整数計画問題における実行可能解の分布の可視化
はじめに
組合せ最適化問題に対するメタヒューリスティクスの設計では,解くべき問題に対して「良い解同士は似通った構造をもっている」という仮定をしばしばおきます[1].この仮定はProximate Optimality Principle(以降,本文ではPOPと略記)とよばれ,メタヒューリスティクスの基本戦略である「探索の集中化」の前提になっています.多くのメタヒューリスティクスは探索の集中化に加え「探索の多様化」とよばれる戦略を適切に組み込むことで高い探索性能の実現を図っています[1][2].
本記事では,私がとくに興味をもっている整数計画問題に話を限定し,実行可能解の分布の可視化を通して,POPの成立性とメタヒューリスティクスでの解きやすさの関係や,集中化と多様化の好適なバランスなどを考察してみたいと思います*1.
なお,本記事の内容は独自研究であり,学会等で広く認められた可視化・分析方法でないこと,どうかあらかじめご容赦いただければ幸いです.正直なところ,記事中にあるような絵を描いたらどうなるかという単純な興味がもともとのモチベーションです.
整数計画問題における実行可能間の距離とProximate Optimality Principle
本記事では,$N$次元の整数ベクトル$\boldsymbol{x}=(x_{1},\dots,x_{N})^{\top}$を決定変数とする(線形)整数計画問題
$$
\begin{aligned}
(\mathrm{IP}): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \boldsymbol{c}^{\top}\boldsymbol{x} \\
\mathrm{subject\,to} \, &\boldsymbol{A}_{1} \boldsymbol{x} \le \boldsymbol{b}_{1}, \\
&\boldsymbol{A}_{2} \boldsymbol{x} = \boldsymbol{b}_{2}, \\
&\boldsymbol{l} \le \boldsymbol{x} \le \boldsymbol{u} , \\
& \boldsymbol{x} \in \mathbb{Z}^{N}
\end{aligned}
$$
を議論の対象とします.(IP)の解$\boldsymbol{x},\boldsymbol{y}\in \mathbb{Z}^{N}$に対し,解間の距離をManhattan距離を用いて$D(\boldsymbol{x},\boldsymbol{y}) = \sum_{n=1}^{N}\lvert x_{n} - y_{n} \rvert$で定義したうえで,解$\boldsymbol{x}$に対する近傍として$\mathcal{N}(\boldsymbol{x}) = \{\boldsymbol{y} \in \mathbb{Z}^{N} | D(\boldsymbol{x},\boldsymbol{y}) =1, \boldsymbol{l} \le \boldsymbol{y} \le \boldsymbol{u} \}
$を採用するメタヒューリスティクスを考えます*2.
(IP)を上述したメタヒューリスティクスで解くとき,以下のような性質を色濃くもつインスタンスほど集中化戦略は有効に作用し,良い解の発見が期待されるといえそうです:
- 近接性: 各実行可能解間の距離が小さい
- 集中性: 目的関数値の小さい実行可能解は特定領域に集中して存在する
近接性・集中性*3の両方が成立するのであれば,既得の暫定解周辺の集中的な探索を繰り返すことにより,最終的に最適解あるいはそれに近い解を得ることが期待できます.いっぽう,たとえば集中性が成り立たず優れた解同士が遠く離れている場合,このような戦略はむしろ逆効果となり,良い解の発見の見込みは薄くなります.本記事では,近接性・集中性の両方の性質が観測されることを,漠然と「POPが成立する」とよぶこととします.
可視化方法
本記事では,以下の3つの方法での可視化を試みることとします.
- (1) 実行可能解間の距離をヒートマップで示す方法
実行可能解間をその目的関数値でソートし,実行可能解間の距離をヒートマップで描画します.もし上述の意味でPOPが成立するのあれば,対角付近の成分の値(目的関数が近い実行可能解間の距離)は小さく,逆に対角から遠い成分の値(目的関数が大きく異なる実行可能解間の距離)は大きくなることが期待されます.
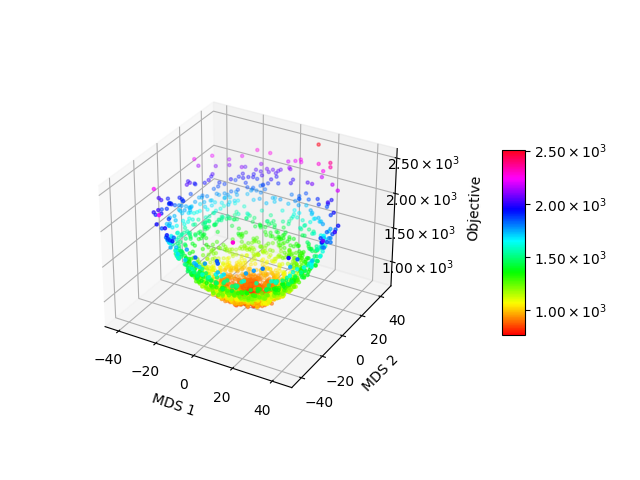
- (2) 多次元尺度構成法を用いる方法
実行可能解間の距離に基づき多次元尺度構成法(Multidimensional Scaling)を用いて実行可能解を2次元に投影し,これに目的関数の軸を加えた3次元の散布図を描画します.POPが成立するのであれば,この散布図の各点は空間内の特定領域に密集しており,また投影された2次元座標に対する目的関数は単純な形状(凸など)であることが期待されます.
- (3) 最小全域木を用いる方法
実行可能解に対応するノード,実行可能解間の距離を重みとしたエッジからなる完全グラフを考え,ここから最小全域木を抽出・描画します.POPが成立するのであれば,最小全域木上において目的関数の近い解(に対応するノード)は互いに近接していることが期待されます.
インスタンス
MIPLIB 2017の整数計画問題インスタンスのうち,a2864-99blp, academictimetablesmall, eilC76-2, t1717を対象とします.各インスタンスの決定変数および制約条件の数を下表に示します.同表におけるカッコ内の数値は冗長な変数や制約を削除した前処理後のものであり,本記事の検討では前処理後のインスタンスに対して実行可能解を求めています.
| No. | インスタンス | 決定変数の数 | 制約条件の数 |
| 1 | a2864-99blp | 200787 (13824) | 22117 (20893) |
| 2 | academictimetablesmall | 28926 (25993) | 23294 (18025) |
| 3 | eilC76-2 | 28599 (28599) | 75 (75) |
| 4 | t1717 | 73885 (16428) | 552 (552) |
ソルバ
実行可能解の抽出には自作メタヒューリスティクスソルバであるPRINTEMPSを用いました.抽出された実行可能解は全実行可能解のごく一部であり,しかもかなりの偏りが存在します.よって,本記事の分析結果はかならずしも各インスタンスの実行可能解全体の性質を議論するものとはならないことにご注意ください.
snowberryfield.hatenadiary.com
可視化結果
以下に,各インスタンスに対する実行可能解分布の可視化結果をサムネイルとして表示しています.拡大するには各画像をクリックします.なお最小全域木の図はgraphvizのneatoレイアウトで描画しており,濃緑色のノードほど目的関数値がより小さい解に対応しています.
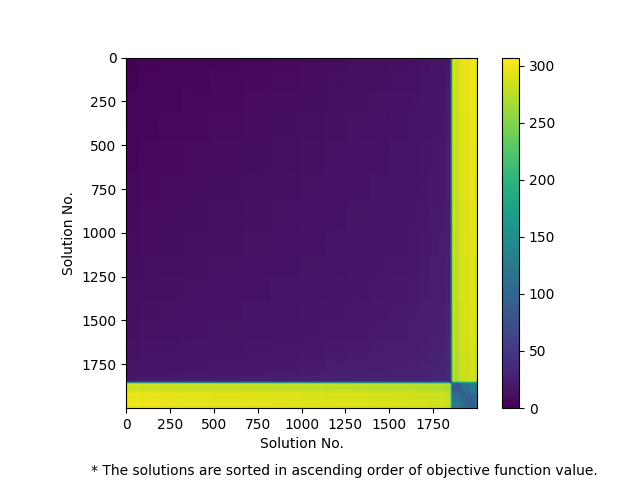


(左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木)



(左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木)


(左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木)



(左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木)
考察
a2864-99blp には大きくわけて2つの局所的最適解があります.ひとつは目的関数値-88のもの(局所的最適解A)で,もうひとつは目的関数値-257のもの(局所的最適解B)で,後者が2021/9/21時点での暫定解となっています.メタヒューリスティクスを適用して先に局所的最適解Aを見つけてしまった場合,そこから脱出することは容易ではなく,局所的最適解Bに到達するには大きな多様化操作を必要とします.図1aや図1bをみると,本インスタンスには局所的最適解Aを含むクラスタ(局所的最適解が密に存在する領域)と局所最適解Bを含むクラスタが存在し,両者は遠く離れていることがわかります.本インスタンスは各局所的最適解のまわりで局所的にみると近接性・集中性の両方が成立するのですが,大域的にみると近接性・集中性ともに満たさないため,大域的な最適解を狙う場合,多様化の弱いメタヒューリスティクスでは解きづらいといえそうです.
academictimetablesmall をメタヒューリスティクスで解こうとすると,小幅な改善の繰り返しではなく,偶発的な大きな改善を主として探索が進行します.図2(b)をみると,目的関数値の大きく異なる実行可能解が互いに離れて存在しており,上述の探索の様相に整合していることがわかります.本インスタンスも上述した近接性・集中性ともに満たさず,メタヒューリスティクスで良い解を得るには多様化の工夫が必要となります.ただし,図2(c)をみると,良い実行可能解同士は基本的には近接しており,探索空間内に不規則に存在しているわけではないことがわかります.したがって,本インスタンスに対しても集中化戦略はやはり有効であり,集中化戦略をベースとしつつ,暫定解の更新が進まない場合に多様化をすこし強める,という方策をとるのが合理的であると考えられます.
eilC76-2とt1717はいずれも集合分割問題です.両者の難易度には大きな差があり,暫定値もしくは最適値に近い解を得るための難易度は圧倒的にt1717のほうが高いです*4.図3(b)をみると,eilC76-2は(多次元尺度構成法で射影された)2次元空間上の中央部に実行可能解が稠密に分布しており,また目的関数値は凸状の形状をしていることから,上述した近接性・集中性の両方を具備している,つまりPOPが成立しているといえそうです.このようなインスタンスの場合,メタヒューリスティクスの集中化戦略は威力を発揮し,実際に解の列挙(探索)の過程においても真の最適値762.5148に対して目的関数値766.134(ギャップ0.4%)の実行可能解を得ることができています.これに対し,図4(a)や図4(b)をみると,t1717の実行可能解はいくつかのクラスタにわかれており,それぞれが互いに離れていることがわかります.このような実行可能解の分布の場合,クラスタ間を移り渡るために大きな多様化が求められるため,集中化に特化したメタヒューリスティクスだとやや分が悪そうです.本検討の列挙(探索)で得られた最良解の目的関数値は168134であり,既知の暫定値(158260)に対して6.2%ものギャップを残しており,多様化が不足している可能性があります.
3つの形式の可視化方法に関して,実行可能解の分布を直観的に把握するという目的に対しては, (1) 実行可能解間の距離をヒートマップで示す方法,(2)多次元尺度構成法を用いる方法,の2つが有用そうです.(3) 最小全域木を用いる方法に関しても,実行可能解同士が離れて存在するようなインスタンスに対して集中的探索を講じることが妥当性かどうかの評価に使えそうです.
おわりに
本記事では,整数計画問題の実行可能解の分布の可視化を試み,その結果,メタヒューリスティクスでの「解きやすさ」の経験則に整合する結果を得ることができました.解きたいインスタンスに対してこのような可視化をおこなうことで,POPの成立性を確認したり,またその結果に基づく多様化・集中化のバランス調整や近傍定義の工夫など,良好な解の取得のための手がかりが得られる可能性もあるのではないかと思います.
なお今回の検討では,メタヒューリスティクスを用いて実行可能解の(偏った)一部を抽出し,それらをもとに可視化・分析をおこなっていますが,本質的には実行可能解の分布はインスタンスデータ($\boldsymbol{A}_{1}, \boldsymbol{A}_{2},\boldsymbol{b}_{1},\boldsymbol{b}_{},\boldsymbol{c},\boldsymbol{l}, \boldsymbol{u}$)により完全に規定されるはずです.インスタンスデータに基づく実行可能解分布の直接的な予言,またそれに基づくアルゴリズム改善(ハイパーパラメータの自動調整など)ができれば面白いと考えており,今後の課題として取り組んでいきたいと考えています.
雑文・長文ではございましたが,最後までお付き合いいただきありがとうございました.