整数計画問題に対する前処理手法とメタヒューリスティクス

数理最適化

本記事は 数理最適化 Advent Calender2022 の25日目（最終日）の記事です．24日目の記事は mirucacule さんによる 最適輸送距離に基づく分布的ロバスト最適化とその周辺 でした。

はじめに

整数計画問題や混合整数計画問題に対する近年のソルバの性能向上の要因として「前処理」がしばしばあげられます．前処理とは，比較的簡単な解析・推論をもとに原問題をより簡単な問題に変換するものであり，たとえば冗長な制約条件を除去する，決定変数のとりうる範囲を狭める（ないしは値を固定する）などの処理が含まれます．本記事では，とくに整数計画問題を対象とした主要な前処理手法を整理したうえで，メタヒューリスティクスを用いて整数計画問題を解く場合の探索性能への影響を確認します．分枝限定法・分枝カット法の性能向上に対する前処理の効果は各種 MIP ソルバにてじゅうぶんに実証されていますが，メタヒューリスティクスを題材とした調査・研究は少ないように思われます． このことが本記事を記した動機のひとつになっています．前回に引き続き，独自研究の色合いが強い記事となりますので，誤りや不正確な部分もあるかもしれません．ご容赦いただければ幸いです．

前処理に関する知見が広く記されたものとしては文献 [1] が有名です．このほか文献 [2] では集合分割問題，集合被覆問題に特化した前処理が整理されています．文献 [1] では，前処理をさらに "Preprocessing" と "Probing" の2つに分類していますが，本記事ではこれらをとくに区別せず，比較的簡単な解析・推論から原問題をより簡単な問題に変換する行為を総称して「前処理」とよぶこととします．

本記事では，各種前処理が有効に作用する具体例を示す目的で，整数計画問題／混合整数計画問題の標準的なベンチマークインスタンス集である MIPLIB 2017 のインスタンスを随所で参照しており，また数値実験にも利用しています．MIPLIB 2017 にはアルゴリズム開発の参考となるインスタンスが揃っており，各インスタンスの特徴に関する情報はそれなりに有益と考えています *1．MIPLIB 2017 の設計指針については文献 [3][4] が詳しく，興味をもたれた方はそちらもご参照いただければと思います。

対象とする問題

本記事では，（線形）整数計画問題

\begin{align}
(\mathrm{IP}): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \sum_{j =1}^{M}c_{j}x_{j} \tag{1} \\
\mathrm{subject\,to} &\sum_{j =1}^{M} a_{ij}x_{j} \le(\ge, =) b_{i} \enspace(i = 1,\dots,N), \tag{2} \\
& l_{j} \le x_{j} \le u_{j} \enspace(j = 1,\dots,M), \tag{3} \\
& x_{j} \in \mathbb{Z} \enspace(j = 1,\dots,M) \tag{4}
\end{align}

を考えます．ただし，$N, M \in \mathbb{N}$ はそれぞれ制約条件と決定変数の数とし，インスタンスを記述するパラメータ$a_{ij}, b_{j}, c_{j}, l_{j}, u_{j}$ $(i=1,\dots,N, \, j=1,\dots,M)$ はいずれも実数とします．なお，議論を単純にするため，各制約条件単独に対しては実行可能解の存在が保証されるものと仮定します．

メタヒューリスティクス

$(\mathrm{IP})$ をメタヒューリスティクス*2を用いて近似的に解くことを考えます．本記事では，現在解 $\boldsymbol{x}$ に対して，上下限制約の範囲内で単一成分の値を $\pm1$ した解の集合 $\{\boldsymbol{x}' \in \mathbb{Z}^{M} \mid D(\boldsymbol{x}',\boldsymbol{x}) =1, \, \boldsymbol{l} \le \boldsymbol{x}' \le \boldsymbol{u} \}$ を基本的な近傍定義として採用するメタヒューリスティクスを想定します．ただし，$D(\boldsymbol{x}',\boldsymbol{x})$ は $\boldsymbol{x}', \boldsymbol{x} \in \mathbb{Z}^{M}$ 間の Manhattan 距離とします．文献 [5][6] などで提案されているアルゴリズムがこれに該当します．このような近傍定義を採用するメタヒューリスティクスでは，等式制約条件が厄介な存在となります．これは，同時に値が変更される変数が限られているために，一度満足した等式制約条件に含まれる決定変数の値を変更しようとする場合，再度の制約違反を余儀なくされるためです．この課題に対して，複数の変数の値を同時に変化させることで制約再違反を起こさずに（あるいは制約違反量を十分小さくしたまま）解を改善させていく工夫 [5][6] も提案されていますが，それだけでは対応しきれないような構造の制約条件も少なからず存在します．したがって， $(\mathrm{IP})$ にメタヒューリスティクスを適用する場合，等式制約条件の削減が大きなポイントとなります．

汎用的な前処理手法

準備

本節では，インスタンスの構造に依存せず適用できる汎用的な前処理手法を紹介します．以降の議論に備え，$(\mathrm{IP})$ を記述する決定変数の添字に関して以下の集合を導入します．

  • $\mathcal{M}_{i}^{+}$ : 値が未固定であり，$i$ 番目の制約条件での係数が正である決定変数の添字集合
  • $\mathcal{M}_{i}^{-}$ : 値が未固定であり，$i$ 番目の制約条件での係数が負である決定変数の添字集合
  • $\mathcal{F}_{i}$ : 値が固定された決定変数のうち，$i$ 番目の制約条件での係数が非零のものの添字集合．固定された決定変数は $\bar{x}_{j}$ のように bar 付きで表記することとします．

各集合の構成要素（添字）は不変ではなく，前処理過程で更新されていくものとし，空集合をとることも許容します．以降ではこれらの集合表記を用いて $i$ 番目の制約を
$$
\sum_{j\in \mathcal{M}_{i}^{+}}a_{ij}x_{j} + \sum_{j\in \mathcal{M}_{i}^{-}}a_{ij}x_{j} + \sum_{j\in \mathcal{F}_{i}}a_{ij}\bar{x}_{j} \le(\ge, =) b_{i} \tag{5}
$$
と書くこととします．さらに，制約条件の番号 $i$ を特定する必要がない場合，あるいは文脈上明らかな場合は添字 $i$ を省略して
$$
\sum_{j\in \mathcal{M}^{+}}a_{j}x_{j} + \sum_{j\in \mathcal{M}^{-}}a_{j}x_{j} + \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} \le(\ge, =) b \tag{6}
$$
と書くこととします（本記事を通じてほとんどがこちらの表記となっているかと思います）．また本記事を通じて以下の表記法を採用します．

  • $u \gets v$: パラメータ $u$ の値を $v$ で更新する（決定変数の上下限の強化など）．
  • $\bar{x} \equiv v$: 変数 $x$ の値を $v$ で固定する．

単一の決定変数や制約条件に着目するもの

本項で述べる前処理は，単一の決定変数や制約条件に着目し，制約関数の上下限値を検証しつつ，冗長な制約条件の除去や決定変数の上下限の強化・固定を図るものです．汎用的な前処理であり，多くの場合，制約条件や決定変数の削減にもっとも大きく貢献します．

本前処理は以下で述べる (1)-(5) のサブ処理から構成されます．なお，ここでは一般性を失わずに不等式制約条件の向きとして $(\le)$ のみを考えることとします．不等号の向きが逆 $(\ge)$ であるとき，以降の処理は適当に修正する必要があることにご注意ください．

(1) 制約条件に含まれない決定変数の値固定

どの制約条件にも含まれない決定変数 $x_{j'}$ がある場合，その値を目的関数の係数の符号に応じて以下のように固定します．
$$
\bar{x}_{j'} \equiv \begin{cases} l_{j'}, \enspace c_{j'} > 0 \\ u_{j'}, \enspace \mathrm{otherwise} \end{cases} \tag{7}
$$

(2) 冗長な制約条件の除去

制約条件が決定変数の値によらず，つねに実行可能となる場合，つまり
$$
\sum_{j\in \mathcal{M}^{+}}a_{j}u_{j} + \sum_{j\in \mathcal{M}^{-}}a_{j}l_{j} + \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} \le b \tag{8}
$$
を満たすとき，あるいは $\mathcal{M}^{+} = \mathcal{M}^{-} =\emptyset$ かつ
$$
\sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} = b \tag{9}
$$
を満たすとき，当該制約を冗長なものとして除去します．

(3) 未固定の決定変数がただ 1 つ含まれる制約条件の除去

未固定の決定変数がただ 1 つ含まれる制約条件に対して，以下の方法で未固定の決定変数 $x_{j'}$ の上下限強化・固定をおこないつつ，当該制約を除去します．

  • 前処理対象が不等式制約条件であり，$x_{j'}$ の係数が正の場合（変数の上限の強化）

$$
u_{j'} \gets \min \left(u_{j'}, \left\lfloor \frac{b - \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j}}{a_{j'}}\right\rfloor\right) \tag{10}
$$

  • 前処理対象が不等式制約条件であり，$x_{j'}$ の係数が負の場合（変数の下限の強化）

$$
l_{j'} \gets \max \left(l_{j'}, \left\lceil \frac{b - \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j}}{a_{j'}}\right\rceil\right) \tag{11}
$$

  • 前処理対象が等式制約条件の場合*3

$$
x_{j'} \equiv \frac{b - \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j}}{a_{j'}} \tag{12}
$$

(4) 決定変数の上下限強化

未固定の決定変数が 2 つ以上含まれる等式・不等式制約条件に対して，決定変数 $x_{j'} \, (j'\in \mathcal{M}^{+}\cup \mathcal{M}^{-})$ の上下限を以下の方法で強化します．ここでは制約条件の除去はできないことに注意します．

  • $x_{j'}$ の係数が正の場合（変数の上限の強化）

$$
u_{j'} \gets \min \left(u_{j'}, \left\lfloor \frac{b - \sum_{j\in \mathcal{M}^{+}\setminus \{ j'\}}a_{j}l_{j} - \sum_{j\in \mathcal{M}^{-}}a_{j}u_{j} - \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j}}{a_{j'}}\right\rfloor\right) \tag{13}
$$

  • $x_{j'}$ の係数が負の場合（変数の下限の強化）

$$
l_{j'} \gets \max \left(l_{j'}, \left\lceil \frac{b - \sum_{j\in \mathcal{M}^{+}}a_{j}u_{j} - \sum_{j\in \mathcal{M}^{-}\setminus \{ j'\}}a_{j}l_{j} - \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j}}{a_{j'}}\right\rceil\right) \tag{14}
$$

(5) 決定変数の固定

決定変数の上下限をチェックし，$l_{j'} = u_{j'}$ となっているものの値を $\bar{x}_{j'} \equiv l_{j'} (= u_{j'})$ と固定します．

これらの処理のうち，とくに (1)-(3) あたりは自明なものであり，果たして意味があるのか（これらが効くインスタンスはあるのか）という疑問が生じるかもしれません．後述するとおり，これらの前処理は各制約条件に対して一度適用して終わりではなく，他の前処理結果の影響を反映しつつ繰り返し適用していくことになります．実際には最初の前処理で (1)-(3) により制約条件や決定変数が除去されることは稀であり，どちらかといえば (4), (5) の結果を受けて (1)-(3) の処理が有効になるというイメージです．

ところで，「前処理」とは少し異なりますが，(4), (5) の処理を最適化計算の実行中に適用することで，（前処理段階ではできなかった）決定変数の上下限強化や固定が可能となる場合もあります．最適化計算の過程で発見した目的関数値の上界値を $\hat{f}$ とするとき，
$$
\sum_{j =1}^{M}c_{j}x_{j} \le \hat{f} \tag{15}
$$
という制約条件を追加しても最適解は変化しないという点に注意します．そこで，上界値が更新されたタイミングで (4), (5) の処理を (15) 式に対して適用します*4．この方法は，一部の決定変数に対する目的関数の係数が非常に大きいインスタンス（Semi-Hard 制約を含むインスタンスなど）や，「最大値最小化」型の構造をとるインスタンスに対して有効です． MIPLIB 2017 Benchmark set のインスタンスではたとえば academictimetablesmall, netdiversion, 30n20b8 に対して効果を発揮します．

複数の制約条件に着目するもの

複数の制約条件に対する前処理のうち，2 つの制約条件の比較に基づく比較的単純なものを紹介します．なおこれらの前処理は，メタヒューリスティクスの探索挙動の改善には直接寄与しません*5．おもに近傍解評価の効率化を意図して実施するものになります．

(1) 不等式制約条件ペアの等式制約条件への統合

$a_j \, (j \in \mathcal{M}^{+} \cup \mathcal{M}^{-})$ および $b$ が完全に同一で，不等式の向きのみが異なる不等式制約条件ペア
\begin{align}
\sum_{j\in \mathcal{M}^{+}}a_{ j}x_{j} + \sum_{j\in \mathcal{M}^{-}}a_{j}x_{j} + \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} \le b \tag{16} \\
\sum_{j\in \mathcal{M}^{+}}a_{ j}x_{j} + \sum_{j\in \mathcal{M}^{-}}a_{j}x_{j} + \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} \ge b \tag{17}
\end{align}
があったとき，これを等式制約条件
$$
\sum_{j\in \mathcal{M}^{+}}a_{j}x_{j} + \sum_{j\in \mathcal{M}^{-}}a_{j}x_{j} + \sum_{j\in \mathcal{F}}a_{j}\bar{x}_{j} = b \tag{18}
$$
として統合します．

(2) 不等式制約条件の重複除去

係数も不等式の向きも完全に同一の不等式制約条件が複数存在する場合，どれかひとつを残して他を除去します．

ところで，2 つの制約条件を対象とした前処理は，ナイーブな実装だと $O(N^2)$ の計算量を要するため，大規模な問題ではかなりの計算時間を必要とします．これを改善する方法としては Hash 値を利用した比較範囲の絞り込みが有効です．具体的な手順は以下のようになります．

  • i) 各制約条件に対して，$a_{j}$ や $b$ の情報をもとに適当な Hash 値を計算しておく．
  • ii) 各制約条件を Hash 値でソートする．
  • iii) Hash 値が同じ制約条件同士に対してのみ，前処理に必要な比較をおこなう．

この方法でも最悪計算量は変わらないのですが，Hash 値が同じとなる（=前処理での比較対象となる）制約条件の数はよほど病的・敵対的なインスタンスでないかぎり僅少であり，ほとんどのインスタンスに対してはこの方法でじゅうぶん高速に処理できます．以降でも複数の制約条件や決定変数を対象とする前処理がいくつか出てきますが，いずれも同様の方法が有効です．

上で述べた，2 つの制約条件の比較に基づく前処理が有効な MIPLIB 2017 Benchmark set のインスタンスには以下のものがあります．個人的には思った以上に多くのインスタンスに効くという印象です．

academictimetablesmall, brazil3, n3div36, neos-2657525-crna, neos-3555904-turama, neos-3988577-wolgan, neos-957323, neos-960392, netdiversion, rail01, rail02, rococoC10-001000, sp97ar

fast0507, n2seq36q, n3div36, cryptanalysiskb128n5obj14, cryptanalysiskb128n5obj16, decomp2, ex10, ex9, highschool1-aigio, hypothyroid-k1, n2seq36q, neos-3555904-turama, sp97ar, supportcase10

特殊な構造・問題に対する前処理手法

本節では，一部の特殊な構造・問題に対して適用可能な前処理手法を紹介します．

集合分割問題・集合被覆問題

集合分割問題 $(\mathrm{SPP})$・集合被覆問題 $(\mathrm{SCP})$ はそれぞれ以下の形式をとる 0-1 整数計画問題です．集合分割問題は等式制約条件のみから構成されるのに対して，集合被覆問題は不等式制約条件 ($\ge$) のみから構成されます*6．

$$
\begin{align}
(\mathrm{SPP}): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \sum_{j=1}^{M} c_{j}x_{j} \tag{19} \\
\mathrm{subject\,to} &\sum_{j =1}^{M} a_{ij}x_{j} = 1 \quad (i = 1,\dots,N), \tag{20} \\
& x_{j} \in \{0,1\} \quad (j = 1,\dots,M), \tag{21} \\
\mathrm{where} \, & a_{ij} \in \{0,1\} \quad (i = 1,\dots,N, \, j=1,\dots,M). \tag{22}
\end{align}
$$

$$
\begin{align}
(\mathrm{SCP}): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \sum_{j=1}^{M} c_{j}x_{j} \tag{23} \\
\mathrm{subject\,to} &\sum_{j =1}^{M} a_{ij}x_{j} \ge 1 \quad (i = 1,\dots,N), \tag{24} \\
& x_{j} \in \{0,1\} \quad (j = 1,\dots,M), \tag{25} \\
\mathrm{where} \, & a_{ij} \in \{0,1\} \quad (i = 1,\dots,N, \, j=1,\dots,M). \tag{26}
\end{align}
$$

以降では，$j$ 番目の決定変数が被覆する制約条件の添字集合を $\mathcal{S}_{j}$ と書き，また $i$ 番目の制約を被覆しうる決定変数の添字集合を $\mathcal{V}_{i}$ と書くことにします．

集合分割問題に対しては，上で述べてきた前処理のほか，以下に示す問題特有の前処理を適用することが可能です．

  • a. $j_{1} \neq j_{2} \, (j_{1}, j_{2} = 1,\dots,M)$ に対して $c_{j_{1}} < c_{j_{2}}$ かつ $\mathcal{S}_{j_{1}} = \mathcal{S}_{j_{2}}$ であるとき，$\bar{x}_{j_2}\equiv 0$ とする．
  • b. $j_{1} < j_{2}\, (j_{1}, j_{2} = 1,\dots,M)$ に対して $c_{j_{1}} \le c_{j_{2}}$ かつ $\mathcal{S}_{j_{1}} = \mathcal{S}_{j_{2}}$ であるとき，$\bar{x}_{j_2}\equiv 0$ とする．
  • c. $i_{1} \neq i_{2}\, (i_{1}, i_{2} = 1,\dots,N)$ に対して $\mathcal{V}_{i_1} \subset \mathcal{V}_{i_2} $ であるとき，$i_2$ 番目の制約条件を除去する．あわせてすべての $j' \in \mathcal{V}_{i_2} \setminus \mathcal{V}_{i_1}$ に対して $\bar{x}_{j'}\equiv 0$ とする．

集合被覆問題に対しても，集合分割問題と類似した以下の前処理を適用することが可能です．

  • a. $j_{1}\neq j_{2}\, (i_{1}, i_{2} = 1,\dots,M)$ に対して $c_{j_{1} }< c_{j_{2}}$ かつ $\mathcal{S}_{j_{2}} \subseteq \mathcal{S}_{j_{1}}$ であるとき，$\bar{x}_{j_2}\equiv 0$ とする．
  • b. $j_{1} < j_{2}\, (i_{1}, i_{2} = 1,\dots,M)$ に対して $c_{j_{1}} \le c_{j_{2}}$ かつ $\mathcal{S}_{j_{2}} \subseteq \mathcal{S}_{j_{1}}$ であるとき，$\bar{x}_{j_2}\equiv 0$ とする．
  • c. $i_{1} \neq i_{2}\, (i_{1}, i_{2} = 1,\dots,N)$ に対して $\mathcal{V}_{i_1} \subset \mathcal{V}_{i_2} $ であるとき，$i_2$ 番目の制約条件を除去する．

これらの前処理が有効な MIPLIB 2017 Benchmark set のインスタンスとして air05 があげられます．また Open インスタンスである大規模な集合分割問題 t1722, t1717, ds-big, ivu06, ivu59 に対しても有効です．これらのインスタンスに対して上述の前処理を適用したときの決定変数削減効果を 表 1 に示しておきます．


表 1 集合分割問題への前処理適用による決定変数削減効果．削減率は前処理前後の決定変数の数をそれぞれ $N_{\mathrm{before}}, N_{\mathrm{after}}$ として，$(1 - N_{\mathrm{after}}/ N_{\mathrm{before}})$ で計算したものです．

No. インスタンス 決定変数（前処理なし） 決定変数（前処理後） 削減率
1 air05
7195
6486
9.85%
2 t1722
36630
6581
82.03%
3 t1717
73885
16428
77.77%
4 ds-big
174997
173029
1.12%
5 ivu06
787239
771919
1.95%
6 ivu59
2569996
2567764
0.09%


中間変数を定義する等式制約条件

整数計画問題のモデリングでは，モデルの記述の見通しのよさを確保するため，中間変数 $y$ の定義に相当する以下のような等式制約条件を導入することがあります．
\begin{align}
y = \sum_{j = 1}^{N} a_{j}x_{j} + b \tag{27} \\
l_{y} \le y \le u_{y} \tag{28}
\end{align}
ただし，$a_{j} \in \mathbb{Z} \, (j = 1,\dots,N), b, l_{y}, u_{y} \in \mathbb{Z}$ とします．このような制約条件がある場合，他式中の $y$ に対して (27) 式を代入し，かわりに 2 つの不等式制約条件
$$
l_{y} \le \sum_{j = 1}^{N} a_{j}x_{j} + b \le u_{y} \tag{29}
$$
を追加することで決定変数 1 つと等式制約条件 1 つを除去できます．ただし，相互に依存関係をもつ中間変数群に対して上述の方法を適用すると，計算手順によっては無限ループが発生する可能性があるため，相互依存関係をもつ中間変数（の定義式）を前処理対象外とするなどの工夫が必要です*7．簡易的な方法としては，候補として抽出された中間変数を頂点，中間変数間の依存の向きを辺とする有向グラフを考え，可到達行列を計算して相互に到達可能な頂点（中間変数）を検知し，前処理対象から除外する方法が考えられます．

上述の手順を，以下の数値例（中間変数を定義する等式制約群）を用いて説明します．ただしここで関心があるのは$y_{1}, y_{2}, y_{3}, y_{4},y_{5}$の配置であり，$x_{1}, x_{2}$に関する項や定数項については（具体例である以上の）意味はありません。

\begin{align}
y_{1} & = 2 x_{1} + 3 x_{2} + 4 \tag{30} \\
y_{2} & = y_{1} + 4 x_{1} - 2 x_{2} + 5 \tag{31} \\
y_{3} & = y_{4} -3 x_{1} + 5 x_{2} - 2 \tag{32} \\
y_{4} & = y_{5} + x_{1} + x_{3} + 3 \tag{33} \\
y_{5} & = y_{3} + 5 x_{1} - 3 x_{2} + 1 \tag{34}
\end{align}
本例では，$y_{1}, y_{2}, y_{3}, y_{4},y_{5}$ が中間変数の候補であり，その依存関係を有向グラフとして表現したときの隣接行列 $\boldsymbol{A}$ と可到達行列 $\boldsymbol{R}$ はそれぞれ以下のようになります．ただし隣接行列の定義では，中間変数 $i$ の定義式に中間変数 $j$ が含まれるとき $a_{ij}=1$，そうでないとき$a_{ij}=0$ としています．
$$
\boldsymbol{A} =\begin{pmatrix}
0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 & 0 \\
\end{pmatrix}, \enspace \boldsymbol{R} =\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
1 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 & 1 \\
0 & 0 & 1 & 1 & 1 \\
0 & 0 & 1 & 1 & 1 \\
\end{pmatrix}
$$
可到達行列 $\boldsymbol{R}$ の非対角成分ペア $(i \neq j )$ に対して $r_{ij}= r_{ji}=1$ であるとき $i, j$（に対応する中間変数）には相互依存関係があります．上の例でいうと $y_{3}, y_{4}, y_{5}$ が互いに依存関係をもっています．そこでこの例の場合では，(31) 式に対する (30) 式の代入のみを実行することにより無限ループを安全に回避できます．

この前処理は，メタヒューリスティクスを用いて $(\mathrm{IP})$ を解く際，一部のインスタンスに対して絶大な威力を発揮するため，個人的におすすめの前処理のひとつです．しかし，上述の方法で抽出される中間変数をすべて除去してよいかというと少し微妙で，とくに 0-1 変数の削除は慎重を期したほうがよいと考えています．性能悪化に繋がりやすい例を 2 つほどあげておきます．

  • a. 2 つの 0-1 変数をつなぐ等式制約条件

（例：$x_{1} = x_{2} \, (x_{1}, x_{2}\in\{0,1\})$）

  • b. スラック変数を含む等式制約条件

（例：$\sum_{j \in \mathcal{J}} x_{j} + y = 1, x_{j} \in \{0, 1\} \, (j \in \mathcal{J}) , y \in \{0, 1\}$, $\mathcal{J}$ は決定変数に関する適当な添字集合，$y$ は大きな正係数 $w$をともなって目的関数に現れるものとします）

まず a. に関して補足します．メタヒューリスティクス分野でよく知られた近傍設計のコツのひとつとして，解の変更をなるべく局所的なものに抑えるというのがあります．複数の 0-1 変数をこの方法でまとめてしまうと，近傍移動によって解の大域的な構造が破壊されるようになり，Proximate Optimality Principle *8に基づく解探索が阻害されるためか，性能が低下してしまう例も多いです．もしこの類の制約に前処理を適用した結果よい性能が出ない場合，特定の 0-1 変数が解の大域的構造に影響しすぎていないかをチェックするのがよいと思います*9．

b. に関しては，目的関数のレンジが本来のものより広くなることに関して注意が必要です*10．制約違反量に対するペナルティ係数を経時的に調整するメタヒューリスティクスを用いる場合，このことが原因でペナルティ係数機構の動作が不安定化する場合があります．

この前処理が有効な MIPLIB 2017 Benchmark set のインスタンスには以下のものがあります．

30n20b8, academictimetablesmall, brazil3, cryptanalysiskb128n5obj14, cryptanalysiskb128n5obj16, highschool1-aigio, hypothyroid-k1, mzzv11, mzzv42z, neos-1354092, neos-2657525-crna, neos-3083819-nubu, neos-662469, neos-950242, proteindesign121hz512p9, proteindesign122trx11p8, rail01, rail02, rococoB10-011000, rococoC10-001000, square41, square47, supportcase19, supportcase6

専用アルゴリズムを適用することで簡単に解ける問題構造

いわゆる「前処理」とは少し違うかもしれませんが，メタヒューリスティクスや分枝限定法を用いずとも，簡単な計算により $(\mathrm{IP})$ の最適解が求まる例をひとつあげておきます．以下の形式をとる 0-1 整数計画問題を考えます．
\begin{align}
(\mathrm{P}_{\mathbb{Z/2Z}}): \underset{\boldsymbol{x}, \boldsymbol{y}}{\mathrm{minimize}} \, & \sum_{j=1}^{N} c_{j}x_{j} \tag{35} \\
\mathrm{subject\,to} &\sum_{j =1}^{N} a_{ij}x_{j} = 2y_{i} + b_{i} \quad (i = 1,\dots,N), \tag{36} \\
& x_{j} \in \{0,1\} \quad (j = 1,\dots,N), \tag{37} \\
& y_{i} \in \mathbb{Z} \quad (i = 1,\dots,N), \tag{38} \\
\mathrm{where} \, & a_{ij} \in \{0,1\} \quad (i,j = 1,\dots,N),\tag{39} \\
\, & b_{i} \in \{0,1\} \quad (i = 1,\dots,N). \tag{40}
\end{align}

制約条件のうち (36) 式は 各式左辺の値が偶数・奇数のどちらであるかを規定するものであり，$y_{i}$ は帳尻をあわせるためのダミー変数です．本制約条件が定める構造は2 元体上の連立方程式と等価であり，これを解くことで（解が存在するのであれば）最適解を求めることができます．2 元体上の連立方程式は Gauss の消去法を用いて解くことできます．具体的な実装については以下のブログ記事に非常にわかりやすい解説と例示があるため，本記事では記述を割愛させていただきます．
drken1215.hatenablog.com

MIPLIB 2017 Benchmark set のインスタンスのうち，enlight_hard がこの構造をとります．その名から類推されるとおり（？）上のブログでも解説されている「ライツアウト (enlight)」とよばれるゲームのインスタンスのようです． enlight_hard は，200 変数という小規模なインスタンスながら，これに類する前処理が組み込まれていない分枝限定法ベースの MIP ソルバではなかなか最適解が求まりません*11．

文脈的にはアルゴリズムというよりはソルバとしての性能向上の議論になりますが，このように，解きやすいアルゴリズムが存在する問題構造の検出を図るアプローチも有効かと思われます．

複数の要素からの選択

整数計画問題では，$ \sum_{j\in \mathcal{J}}x_{j} = 1$ という形式の制約条件（Set Partitioning 制約）が頻出します．ただし ${\mathcal{J}}$ は適当な添字集合で，$x_{j} \, (j \in \mathcal{J})$ は 0-1 変数であるとします． Set Partitioning 制約はその名のとおり，上述した集合分割問題を記述する制約条件でもあるのですが，「複数の要素からちょうどひとつを選択する」という意図で用いられることも多く，スケジューリング問題等で頻出します．本記事ではこの意図で用いられている Set Partitioning 制約を Selection 制約とよぶことにします．Selection 制約に対しては，「${\mathcal{J}}$ のなかで値 1 をとる変数を交換する」という近傍の定義を採用することで，当該制約を遵守したまま近傍探索が可能となります．

ひとつ注意しなければならないのは，Selection 制約が複数あり，それぞれに対応する添字集合同士が共通部分をもつケースです．この場合，上述の方法による近傍定義はできないため，独立した添字集合の組合せを抽出する必要があります．具体的な方法としてはたとえば

  • a. 添字集合の独立性を維持しつつ，適当な順番（制約条件番号，添字集合の要素数の大小など）で抽出するもの
  • b. はじめから他のすべての Selection 制約と独立しているもののみを抽出するもの
  • c. この問題自体を組合せ最適化問題（集合パッキング問題）として定式化して解いて求めるもの

などが考えられます．経験的には b. がモデリングの思想（Selection 制約としての意図）を一番うまく抽出でき，性能面でも優れていることが多いように思います．上述のうち b. の方法を用いた場合に Selection 制約が抽出される MIPLIB 2017 Benchmark set のインスタンスには以下のものがあります．

academictimetablesmall, bab6, neos-1354092, netdiversion, neos-4738912-atrato, neos-3004026-krka, decomp2, highschool1-aigio, brazil3, 30n20n8, supportcase6, co-100, proteindesign121hz512p9,
proteindesign122trx11p8, rail02, rococoC10-001000, n2seq36q, rail01, bab2, chromaticindex512-7, chromaticindex1024-7

前処理の流れ

個別の前処理手法を組み込んだ，全体としての前処理の流れについて整理しておきます．これまで述べてきた各前処理手法はその結果が互いに影響を及ぼします．一度実行した前処理であっても，他の手法において改善（制約条件の除去や決定変数の上下限強化・固定）があった場合に，これを再度実行することでさらなる改善が得られるケースもあります．したがって，前処理全体のプロセスとしては，各手法を順番に繰り返し適用し，最終的にどの手法を適用しても改善がみられなくなった段階で処理を終了します．

前処理の効果

本記事で紹介した前処理の効果を数値実験で確認します．インスタンスとしては MIPLIB 2017 Benchmark set のうち純整数計画問題 89 インスタンス，メタヒューリスティクスソルバとしては重み付け Tabu Search [7] に基づく自作整数計画ソルバ PRINTEMPS を使用しました．

github.com

その他詳細な計算条件は以下のとおりです．

図 1 に，前処理適用による決定変数・制約条件の削減効果を示します．また 表 2 に，各インスタンスに対する具体的な前処理前後の決定変数・制約条件の数と，前処理の有無それぞれのもと得られた目的関数値（制約違反量）を示します．表 2では，オープンソースの MIP ソルバである CBC 2.10.8 を同一計算環境・計算条件のもと各インスタンスに適用して得られた結果もあわせて示しています．ただしこれは，メタヒューリスティクスがインスタンスによっては （よい上界値を得るという意味で）MIP ソルバに比肩することを例示するためであり，ソルバ全体としての性能評価を目的としたものではないことを強調しておきます*13．よって，以降でも CBC の結果についてはとくに議論しないこととします。



図 1 MIPLIB 2017 Benchmark set のうち純整数計画問題 89 インスタンスに対する，前処理適用による決定変数・制約条件の削減効果の散布図．削減率 は前処理前後の決定変数（制約条件）の数をそれぞれ $N_{\mathrm{before}}, N_{\mathrm{after}}$ として，$(1 - N_{\mathrm{after}}/ N_{\mathrm{before}})$ で計算したものです．


表 2 MIPLIB 2017 Benchmark set のうち純整数計画問題 89 インスタンスに対する数値実験結果詳細．目的関数値（制約違反量）については，実行可能解が得られた場合は暫定解における目的関数値を黒字で，そうでない場合は到達できた制約違反量の最小値を丸括弧付きの赤字で示しています．目的関数値（制約違反量）の各列で先頭に "*" が付せられているものは最適性あるいは実行不可能性を証明できたことを意味します*14．


No. インスタンス 決定変数 制約条件 目的関数値（制約違反量）
前処理なし 前処理後 前処理なし 前処理後 前処理なし 前処理後 CBC 2.10.8 最適値
1 reblock115 1150 1150 4735 4735 -3.553e+07 -3.553e+07 -3.674e+07 -3.680e+07
2 academictimetablesmall 28926 25993 23294 17624 (1.200e+01) 6.720e+02 (no solution) 0.000e+00
3 bab6 114240 114240 29904 29883 (6.300e+01) (5.600e+01) (no solution) -2.842e+05
4 gen-ip002 41 41 24 24 -4.784e+03 -4.784e+03 *-4.784e+03 -4.784e+03
5 gen-ip054 30 30 27 27 6.841e+03 6.853e+03 6.841e+03 6.841e+03
6 comp21-2idx 10863 10752 14038 13961 1.080e+02 1.090e+02 (no solution) 7.400e+01
7 comp07-2idx 17264 17187 21235 21189 8.000e+00 8.000e+00 (no solution) 6.000e+00
8 neos859080 160 160 164 160 (1.000e+00) (1.000e+00) (no solution) Infeasible
9 neos-787933 236376 236376 1897 1897 3.800e+01 3.800e+01 3.000e+01 3.000e+01
10 air05 7195 6486 426 358 2.658e+04 2.645e+04 *2.637e+04 2.637e+04
11 mzzv42z 11717 11717 10460 10511 -1.684e+04 -1.881e+04 *-2.054e+04 -2.054e+04
12 nu25-pr12 5868 5834 2313 2274 5.536e+04 5.482e+04 *5.390e+04 5.390e+04
13 irp 20315 19370 39 39 1.216e+04 1.216e+04 *1.216e+04 1.216e+04
14 qap10 4150 4150 1820 1820 3.640e+02 3.640e+02 *3.400e+02 3.400e+02
15 neos8 23228 23116 46324 46212 -3.717e+03 -3.717e+03 *-3.719e+03 -3.719e+03
16 sp98ar 15085 15085 1435 1429 5.472e+08 5.466e+08 5.306e+08 5.297e+08
17 neos-960392 59376 59376 4744 4230 -2.380e+02 -2.380e+02 *-2.380e+02 -2.380e+02
18 enlight_hard 200 0 100 100 (1.000e+00) *3.700e+01 *3.700e+01 3.700e+01
19 neos-1582420 10100 10100 10180 10180 9.500e+01 9.500e+01 *9.100e+01 9.100e+01
20 fast0507 63009 63002 507 484 1.770e+02 1.780e+02 *1.740e+02 1.740e+02
21 neos-950242 5760 5760 34224 33984 (1.000e+00) 4.000e+00 *4.000e+00 4.000e+00
22 neos-662469 18235 18235 1085 1085 2.155e+05 3.457e+05 1.844e+05 1.844e+05
23 neos-957323 57756 57756 3757 3243 -2.377e+02 -2.377e+02 *-2.378e+02 -2.378e+02
24 nw04 87482 46190 36 36 1.690e+04 1.704e+04 *1.686e+04 1.686e+04
25 neos-1354092 13702 13702 3135 1666 (2.000e+00) 4.800e+01 5.500e+01 4.600e+01
26 mzzv11 10240 10240 9499 9544 -1.863e+04 -1.956e+04 *-2.172e+04 -2.172e+04
27 netdiversion 129180 129180 119589 99913 (2.000e+00) (2.000e+00) 3.840e+02 2.420e+02
28 sorrell3 1024 1024 169162 169162 -1.600e+01 -1.600e+01 (no solution) -1.600e+01
29 bnatt400 3600 2003 5614 4006 (3.577e+00) (2.593e+00) (no solution) 1.000e+00
30 tbfp-network 72747 72747 2436 2436 2.916e+01 2.916e+01 2.687e+01 2.416e+01
31 glass-sc 214 214 6119 6119 2.300e+01 2.300e+01 2.300e+01 2.300e+01
32 ex9 10404 8560 40962 33779 (4.000e+01) 8.100e+01 (no solution) 8.100e+01
33 neos-3024952-loue 3255 3255 3705 3705 1.145e+05 1.171e+05 (no solution) 2.676e+04
34 neos-4738912-atrato 6216 6216 1947 1939 3.300e+08 3.193e+08 2.851e+08 2.836e+08
35 neos-3083819-nubu 8644 7940 4725 4183 6.611e+06 6.591e+06 *6.308e+06 6.308e+06
36 neos-2657525-crna 524 522 342 307 (7.659e-01) 1.811e+00 1.373e+01 1.811e+00
37 neos-3381206-awhea 2375 2375 479 479 4.530e+02 4.530e+02 *4.530e+02 4.530e+02
38 neos-5052403-cygnet 32868 27642 38268 38268 2.010e+02 2.010e+02 (no solution) 1.820e+02
39 neos-3004026-krka 17030 17030 12545 8320 *0.000e+00 *0.000e+00 (no solution) 0.000e+00
40 nursesched-sprint02 10250 10210 3522 3512 6.100e+01 6.200e+01 *5.800e+01 5.800e+01
41 nursesched-medium-hint03 34248 33990 14062 13672 6.790e+02 8.170e+02 (no solution) 1.150e+02
42 sp97ar 14101 14101 1761 1705 6.814e+08 6.776e+08 6.704e+08 6.607e+08
43 graph20-20-1rand 2183 2146 5587 5180 -9.000e+00 -9.000e+00 -8.000e+00 -9.000e+00
44 wachplan 3361 3004 1553 1423 -8.000e+00 -8.000e+00 -8.000e+00 -8.000e+00
45 decomp2 14379 14379 10765 8473 -1.600e+02 *-1.600e+02 *-1.600e+02 -1.600e+02
46 highschool1-aigio 320404 305241 92568 82741 (8.408e+03) (9.282e+03) (no solution) 0.000e+00
47 brazil3 23968 17802 14646 10000 (5.100e+01) 3.340e+02 9.700e+01 2.400e+01
48 eilA101-2 65832 65832 100 100 1.003e+03 1.003e+03 1.276e+03 8.809e+02
49 30n20b8 11098 8033 576 519 (5.000e+00) 3.020e+02 (no solution) 3.020e+02
50 supportcase18 13410 13410 240 240 4.900e+01 4.900e+01 5.100e+01 4.800e+01
51 supportcase6 130052 130052 771 769 6.240e+04 6.228e+04 5.198e+04 5.191e+04
52 supportcase22 7129 7129 260602 260602 (1.000e+00) (1.000e+00) (no solution) Infeasible
53 supportcase10 14770 14594 165684 165272 (7.510e+02) (7.700e+02) (no solution) 7.000e+00
54 supportcase19 1429098 1429097 10713 10833 (6.000e+00) (8.000e+00) (no solution) 1.268e+07
55 n3div36 22120 22120 4484 4455 1.314e+05 1.314e+05 1.310e+05 1.308e+05
56 cvs16r128-89 3472 3472 4633 4633 -9.400e+01 -9.400e+01 -9.300e+01 -9.700e+01
57 co-100 48417 48114 2187 2104 2.772e+06 2.752e+06 6.136e+06 2.640e+06
58 lectsched-5-obj 21805 10623 38884 16701 (2.817e+03) 3.600e+01 (no solution) 2.400e+01
59 neos-3555904-turama 37461 33362 146493 107302 (1.000e+00) (1.000e+00) (no solution) -3.470e+01
60 neos-3988577-wolgan 25870 25870 44662 44147 (8.000e+00) (7.000e+00) *Infeasible Infeasible
61 neos-2075418-temuka 122304 122304 349602 349602 (4.170e+02) (4.170e+02) (no solution) Infeasible
62 splice1k1 3253 3253 6505 6504 -3.600e+01 -3.220e+02 (no solution) -3.940e+02
63 hypothyroid-k1 2599 2599 5195 5189 -2.851e+03 -2.851e+03 -2.851e+03 -2.851e+03
64 cryptanalysiskb128n5obj16 47622 44144 98021 77093 (2.832e+03) (1.499e+03) (no solution) 0.000e+00
65 proteindesign121hz512p9 159145 78360 301 159 (6.800e+01) 1.488e+03 (no solution) 1.473e+03
66 k1mushroom 8210 8210 16419 16418 -1.136e+03 -3.288e+03 (no solution) -3.288e+03
67 cryptanalysiskb128n5obj14 47622 44144 98021 77039 (7.010e+02) (3.430e+02) (no solution) Infeasible
68 proteindesign122trx11p8 127326 74963 254 169 (3.700e+01) 1.752e+03 1.757e+03 1.747e+03
69 peg-solitaire-a3 4552 4199 4587 4232 (3.000e+00) (1.000e+00) (no solution) 1.000e+00
70 cod105 1024 1024 1024 1024 -1.200e+01 -1.200e+01 -1.200e+01 -1.200e+01
71 supportcase33 20196 7381 20489 3729 -9.500e+01 -1.350e+02 -1.600e+02 -3.450e+02
72 rail02 270869 270867 95791 95628 (1.800e+01) (1.500e+01) (no solution) -2.004e+02
73 ns1952667 13264 13263 41 40 (2.600e+01) (2.200e+01) (no solution) 0.000e+00
74 seymour 1372 1255 4944 4827 4.240e+02 4.240e+02 4.280e+02 4.230e+02
75 ex10 17680 15936 69608 62976 (5.400e+01) (5.200e+01) (no solution) 1.000e+02
76 rococoC10-001000 3117 2566 1293 570 (6.600e+01) 1.171e+04 1.146e+04 1.146e+04
77 n2seq36q 22480 22480 2565 2411 5.600e+04 5.240e+04 5.220e+04 5.220e+04
78 bnatt500 4500 2529 7029 5058 (4.577e+00) (2.968e+00) (no solution) Infeasible
79 s100 364417 334736 14733 14057 -1.428e-01 -1.387e-01 (no solution) -1.697e-01
80 opm2-z10-s4 6250 6250 160633 160633 -3.013e+04 -3.013e+04 -1.874e+03 -3.327e+04
81 square47 95030 35733 61591 2251 (2.000e+00) 5.200e+01 (no solution) 1.600e+01
82 square41 62234 23828 40160 1717 (2.000e+00) 2.200e+01 (no solution) 1.500e+01
83 rail01 117527 117526 46843 46706 (1.500e+01) (2.200e+01) (no solution) -7.057e+01
84 rococoB10-011000 4456 3646 1667 720 (8.300e+01) 2.515e+04 2.126e+04 1.945e+04
85 neos-631710 167056 167056 169576 169576 2.060e+02 2.060e+02 (no solution) 2.030e+02
86 bab2 147912 146248 17245 16986 (7.300e+01) (8.800e+01) (no solution) -3.575e+05
87 chromaticindex512-7 36864 36864 33791 24576 4.000e+00 4.000e+00 4.000e+00 4.000e+00
88 chromaticindex1024-7 73728 73728 67583 49152 4.000e+00 4.000e+00 4.000e+00 4.000e+00
89 eil33-2 4516 4516 32 32 9.340e+02 9.340e+02 *9.340e+02 9.340e+02


図 1 は，$x$ 軸，$y$ 軸の値が大きいプロット（に対応するインスタンス）ほど，前処理による決定変数・制約条件の削減効果が大きいことを示しています．前処理効果のないインスタンスも多いですが，決定変数や制約条件のうち半分近くが削減できるインスタンスも稀ではないことが見てとれるかと思います．ちなみに決定変数の削減率が 100% となっているのは前掲の enlight_hard です．

表 2 をみると，前処理の適用により，全体的に性能が改善していることがわかります．とくに前処理なしでは実行可能解が得られていなかったインスタンスのうち 15 題に対して，実行可能解を得ることに成功しており，メタヒューリスティクスに対しても前処理は重要であるということが確認できました．性能向上に対する貢献が比較的大きいのは「複数要素からの選択」に対する特殊近傍の採用であり，ついで中間変数の削除があげられます．これらはメタヒューリスティクスにとっては実質的に近傍構造を変化させるものであり，「近傍定義が重要」というメタヒューリスティクス設計のセオリーの実証にもなっているかと思います．

おわりに

個人的に思う前処理の面白いところは 「単純なルールが相互に影響しあって大きな効果を生む」という点にあります．正直なところ，整数計画ソルバを開発し始めた当初は前処理をあまり重要視していなかったのですが，一度実装してその効果を確認したとき，とても感動したのを覚えています．本記事を通じて前処理の面白さが少しでも伝われば幸いです．

長くなってしまいましたが，最後までお付き合いいただきありがとうございました．それではよいお年をお過ごしください．

参考文献

*1:個人的によくお世話になっているのは academictimetablesmall, ex9, neos-2657525-crna, brazil3, lectsched-5-obj の5題です．

*2:正確には「メタヒューリスティクス」は具体的なアルゴリズムを指すものではなく，ヒューリスティクスを設計・実装するための汎用的なアイデア群のことを指します．ただし本記事では「メタヒューリスティクスに基づいて設計・実装されたヒューリスティクス」のことを指してメタヒューリスティクスとよぶこととします．

*3:ここで右辺が整数とならなかった場合はその時点でインスタンスが実行不可能性が示せたことになります．実行不可能性を許容しつつ探索を継続したい場合には右辺の値を適当に整数にまるめて $x_{j'}$ の値として固定するなどの方法が考えられます．

*4:前処理後に (15) 式を制約条件として残すべきか，除去すべきかについては慎重な議論がいりそうです．残す場合，アルゴリズム設計・実装において整合性を気にするべき点が多数出てくるため，個人的には除去する方法が好みです．

*5:ただし，制約違反量の計算結果が変わるので，探索の様相は変わります．

*6:不等号の向きが ($\le$) となった問題は「集合パッキング問題」とよばれます．こちらについても本記事に記載したものと同様の前処理を考えることができますが，割愛させていただきます．

*7:このほかにもたとえば，複数の制約で同じ記号の中間変数が抽出された場合の扱いなどにも注意を要しますが，本記事では割愛します．

*8:「良い解同士は似通った構造をもっている」という仮定で，しばしばメタヒューリスティクス設計の前提としておかれます．

*9:0-1 変数をつなぐ等式制約条件であっても $x_{1} + x_{2} = 1$ の形式のものについては，片方の変数を削除してもとくに大きな問題は生じないことが多い気がします…なぜ…．

*10:目的関数中の $y$ に $1- \sum_{j \in \mathcal{J}} x_{j} $ を代入すると，当該部分のレンジが本来 $[0, w]$ だったものが $[w (1- \lvert \mathcal{J}\rvert), w]$ になります．

*11:ただし聞くところによると SCIP には上述の処理が実装されているようで，ただちに最適解が得られます．

*12:計算時間にファイル読み込み処理分は含んでいません．前処理分は含んでいます．

*13: メタヒューリスティクスが（少なくとも本例において）上界値の更新だけをタスクとするのに対して，CBCをはじめとする MIP ソルバは下界値の更新やそれに基づく最適性・実行不可能性の証明もタスクとして担っているため，上界値のみを参照した性能比較は適切ではないと考えています．

*14:適用したメタヒューリスティクスは， $(\mathrm{IP})$ のインスタンスに対し一般に最適性や実行不可能性の証明をすることはできませんが，ある実行可能解においてどの変数を操作しても目的関数値を改善できない場合はその実行可能解を最適解として結論付けられます．

整数計画問題における実行可能解の分布の可視化

数理最適化

はじめに

組合せ最適化問題に対するメタヒューリスティクスの設計では，解くべき問題に対して「良い解同士は似通った構造をもっている」という仮定をしばしばおきます[1]．この仮定はProximate Optimality Principle（以降，本文ではPOPと略記）とよばれ，メタヒューリスティクスの基本戦略である「探索の集中化」の前提になっています．多くのメタヒューリスティクスは探索の集中化に加え「探索の多様化」とよばれる戦略を適切に組み込むことで高い探索性能の実現を図っています[1][2]．

本記事では，私がとくに興味をもっている整数計画問題に話を限定し，実行可能解の分布の可視化を通して，POPの成立性とメタヒューリスティクスでの解きやすさの関係や，集中化と多様化の好適なバランスなどを考察してみたいと思います*1．

なお，本記事の内容は独自研究であり，学会等で広く認められた可視化・分析方法でないこと，どうかあらかじめご容赦いただければ幸いです．正直なところ，記事中にあるような絵を描いたらどうなるかという単純な興味がもともとのモチベーションです．

整数計画問題における実行可能間の距離とProximate Optimality Principle

本記事では，$N$次元の整数ベクトル$\boldsymbol{x}=(x_{1},\dots,x_{N})^{\top}$を決定変数とする（線形）整数計画問題
$$
\begin{aligned}
(\mathrm{IP}): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \boldsymbol{c}^{\top}\boldsymbol{x} \\
\mathrm{subject\,to} \, &\boldsymbol{A}_{1} \boldsymbol{x} \le \boldsymbol{b}_{1}, \\
&\boldsymbol{A}_{2} \boldsymbol{x} = \boldsymbol{b}_{2}, \\
&\boldsymbol{l} \le \boldsymbol{x} \le \boldsymbol{u} , \\
& \boldsymbol{x} \in \mathbb{Z}^{N}
\end{aligned}
$$
を議論の対象とします．(IP)の解$\boldsymbol{x},\boldsymbol{y}\in \mathbb{Z}^{N}$に対し，解間の距離をManhattan距離を用いて$D(\boldsymbol{x},\boldsymbol{y}) = \sum_{n=1}^{N}\lvert x_{n} - y_{n} \rvert$で定義したうえで，解$\boldsymbol{x}$に対する近傍として$\mathcal{N}(\boldsymbol{x}) = \{\boldsymbol{y} \in \mathbb{Z}^{N} | D(\boldsymbol{x},\boldsymbol{y}) =1, \boldsymbol{l} \le \boldsymbol{y} \le \boldsymbol{u} \}
$を採用するメタヒューリスティクスを考えます*2．

(IP)を上述したメタヒューリスティクスで解くとき，以下のような性質を色濃くもつインスタンスほど集中化戦略は有効に作用し，良い解の発見が期待されるといえそうです：

  • 近接性： 各実行可能解間の距離が小さい
  • 集中性： 目的関数値の小さい実行可能解は特定領域に集中して存在する

近接性・集中性*3の両方が成立するのであれば，既得の暫定解周辺の集中的な探索を繰り返すことにより，最終的に最適解あるいはそれに近い解を得ることが期待できます．いっぽう，たとえば集中性が成り立たず優れた解同士が遠く離れている場合，このような戦略はむしろ逆効果となり，良い解の発見の見込みは薄くなります．本記事では，近接性・集中性の両方の性質が観測されることを，漠然と「POPが成立する」とよぶこととします．

可視化方法

本記事では，以下の3つの方法での可視化を試みることとします．

  • (1) 実行可能解間の距離をヒートマップで示す方法

実行可能解間をその目的関数値でソートし，実行可能解間の距離をヒートマップで描画します．もし上述の意味でPOPが成立するのあれば，対角付近の成分の値（目的関数が近い実行可能解間の距離）は小さく，逆に対角から遠い成分の値（目的関数が大きく異なる実行可能解間の距離）は大きくなることが期待されます．

  • (2) 多次元尺度構成法を用いる方法

実行可能解間の距離に基づき多次元尺度構成法(Multidimensional Scaling)を用いて実行可能解を2次元に投影し，これに目的関数の軸を加えた3次元の散布図を描画します．POPが成立するのであれば，この散布図の各点は空間内の特定領域に密集しており，また投影された2次元座標に対する目的関数は単純な形状（凸など）であることが期待されます．

実行可能解に対応するノード，実行可能解間の距離を重みとしたエッジからなる完全グラフを考え，ここから最小全域木を抽出・描画します．POPが成立するのであれば，最小全域木上において目的関数の近い解（に対応するノード）は互いに近接していることが期待されます．
　

インスタンス

MIPLIB 2017の整数計画問題インスタンスのうち，a2864-99blp, academictimetablesmall, eilC76-2, t1717を対象とします．各インスタンスの決定変数および制約条件の数を下表に示します．同表におけるカッコ内の数値は冗長な変数や制約を削除した前処理後のものであり，本記事の検討では前処理後のインスタンスに対して実行可能解を求めています．

No. インスタンス 決定変数の数 制約条件の数
1 a2864-99blp 200787 (13824) 22117 (20893)
2 academictimetablesmall 28926 (25993) 23294 (18025)
3 eilC76-2 28599 (28599) 75 (75)
4 t1717 73885 (16428) 552 (552)

ソルバ

実行可能解の抽出には自作メタヒューリスティクスソルバであるPRINTEMPSを用いました．抽出された実行可能解は全実行可能解のごく一部であり，しかもかなりの偏りが存在します．よって，本記事の分析結果はかならずしも各インスタンスの実行可能解全体の性質を議論するものとはならないことにご注意ください．
snowberryfield.hatenadiary.com

可視化結果

以下に，各インスタンスに対する実行可能解分布の可視化結果をサムネイルとして表示しています．拡大するには各画像をクリックします．なお最小全域木の図はgraphvizのneatoレイアウトで描画しており，濃緑色のノードほど目的関数値がより小さい解に対応しています．

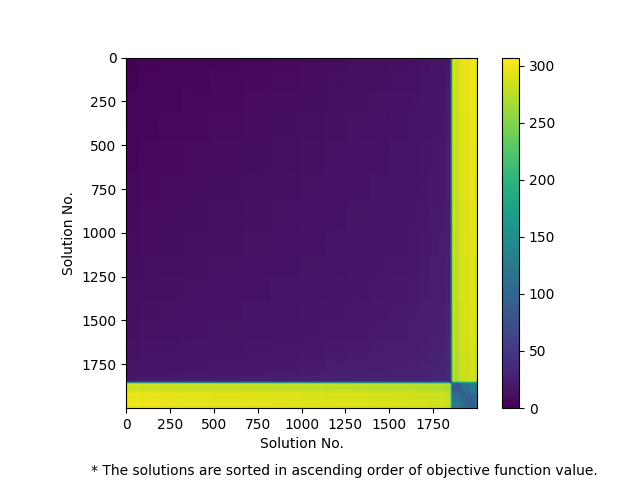
f:id:snowberryfield:20210920224838p:plain f:id:snowberryfield:20210920224847p:plain f:id:snowberryfield:20210920233406p:plain
図1 a2864-99blp 実行可能解の分布（可視化対象実行可能解数：2000）
（左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木）
f:id:snowberryfield:20210920225553p:plain f:id:snowberryfield:20210920225618p:plain f:id:snowberryfield:20210920233456p:plain
図2 academictimetablesmall 実行可能解の分布（可視化対象実行可能解数：674）
（左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木）
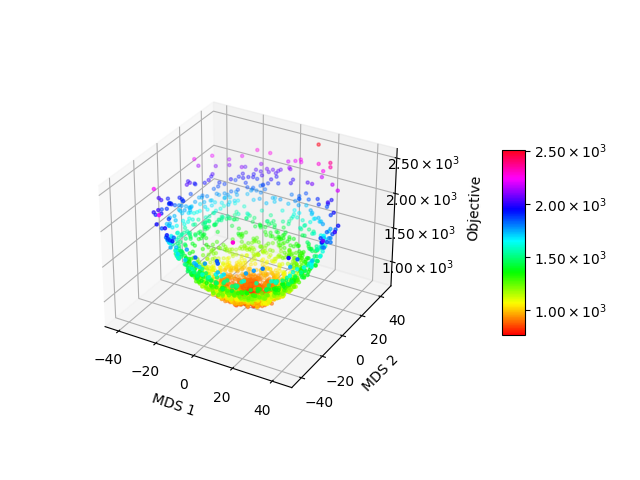
f:id:snowberryfield:20210920233610p:plain f:id:snowberryfield:20210920233632p:plain f:id:snowberryfield:20210920233649p:plain
図3 eilC76-2実行可能解の分布（可視化対象実行可能解数：2127）
（左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木）
f:id:snowberryfield:20210920230049p:plain f:id:snowberryfield:20210920230128p:plain f:id:snowberryfield:20210920233533p:plain
図4 t1717実行可能解の分布（可視化対象実行可能解数：634）
（左からa:ヒートマップ, b:多次元尺度構成法, c: 最小全域木）

考察

a2864-99blp には大きくわけて2つの局所的最適解があります．ひとつは目的関数値-88のもの（局所的最適解A)で，もうひとつは目的関数値-257のもの（局所的最適解B）で，後者が2021/9/21時点での暫定解となっています．メタヒューリスティクスを適用して先に局所的最適解Aを見つけてしまった場合，そこから脱出することは容易ではなく，局所的最適解Bに到達するには大きな多様化操作を必要とします．図1aや図1bをみると，本インスタンスには局所的最適解Aを含むクラスタ（局所的最適解が密に存在する領域）と局所最適解Bを含むクラスタが存在し，両者は遠く離れていることがわかります．本インスタンスは各局所的最適解のまわりで局所的にみると近接性・集中性の両方が成立するのですが，大域的にみると近接性・集中性ともに満たさないため，大域的な最適解を狙う場合，多様化の弱いメタヒューリスティクスでは解きづらいといえそうです．

academictimetablesmall をメタヒューリスティクスで解こうとすると，小幅な改善の繰り返しではなく，偶発的な大きな改善を主として探索が進行します．図2(b)をみると，目的関数値の大きく異なる実行可能解が互いに離れて存在しており，上述の探索の様相に整合していることがわかります．本インスタンスも上述した近接性・集中性ともに満たさず，メタヒューリスティクスで良い解を得るには多様化の工夫が必要となります．ただし，図2(c)をみると，良い実行可能解同士は基本的には近接しており，探索空間内に不規則に存在しているわけではないことがわかります．したがって，本インスタンスに対しても集中化戦略はやはり有効であり，集中化戦略をベースとしつつ，暫定解の更新が進まない場合に多様化をすこし強める，という方策をとるのが合理的であると考えられます．

eilC76-2とt1717はいずれも集合分割問題です．両者の難易度には大きな差があり，暫定値もしくは最適値に近い解を得るための難易度は圧倒的にt1717のほうが高いです*4．図3(b)をみると，eilC76-2は（多次元尺度構成法で射影された）2次元空間上の中央部に実行可能解が稠密に分布しており，また目的関数値は凸状の形状をしていることから，上述した近接性・集中性の両方を具備している，つまりPOPが成立しているといえそうです．このようなインスタンスの場合，メタヒューリスティクスの集中化戦略は威力を発揮し，実際に解の列挙（探索）の過程においても真の最適値762.5148に対して目的関数値766.134（ギャップ0.4%）の実行可能解を得ることができています．これに対し，図4(a)や図4(b)をみると，t1717の実行可能解はいくつかのクラスタにわかれており，それぞれが互いに離れていることがわかります．このような実行可能解の分布の場合，クラスタ間を移り渡るために大きな多様化が求められるため，集中化に特化したメタヒューリスティクスだとやや分が悪そうです．本検討の列挙（探索）で得られた最良解の目的関数値は168134であり，既知の暫定値（158260）に対して6.2%ものギャップを残しており，多様化が不足している可能性があります．

3つの形式の可視化方法に関して，実行可能解の分布を直観的に把握するという目的に対しては， (1) 実行可能解間の距離をヒートマップで示す方法，(2)多次元尺度構成法を用いる方法，の2つが有用そうです．(3) 最小全域木を用いる方法に関しても，実行可能解同士が離れて存在するようなインスタンスに対して集中的探索を講じることが妥当性かどうかの評価に使えそうです．

おわりに

本記事では，整数計画問題の実行可能解の分布の可視化を試み，その結果，メタヒューリスティクスでの「解きやすさ」の経験則に整合する結果を得ることができました．解きたいインスタンスに対してこのような可視化をおこなうことで，POPの成立性を確認したり，またその結果に基づく多様化・集中化のバランス調整や近傍定義の工夫など，良好な解の取得のための手がかりが得られる可能性もあるのではないかと思います．

なお今回の検討では，メタヒューリスティクスを用いて実行可能解の（偏った）一部を抽出し，それらをもとに可視化・分析をおこなっていますが，本質的には実行可能解の分布はインスタンスデータ（$\boldsymbol{A}_{1}, \boldsymbol{A}_{2},\boldsymbol{b}_{1},\boldsymbol{b}_{},\boldsymbol{c},\boldsymbol{l}, \boldsymbol{u}$）により完全に規定されるはずです．インスタンスデータに基づく実行可能解分布の直接的な予言，またそれに基づくアルゴリズム改善（ハイパーパラメータの自動調整など）ができれば面白いと考えており，今後の課題として取り組んでいきたいと考えています．

雑文・長文ではございましたが，最後までお付き合いいただきありがとうございました．

参考文献

  • [1] 柳浦睦憲，茨木俊秀「組合せ最適化 ーメタ戦略を中心としてー」朝倉書店 (2001)
  • [2] 梅谷俊治「しっかり学ぶ数理最適化 モデルからアルゴリズムまで」講談社 (2020)

*1:本記事において「解きやすさ」とは「（最適性の証明のない）そこそこ良い実行可能解を得やすいかどうか」を漠然と意味することとします．

*2:$\mathcal{N}(\boldsymbol{x})$は$\boldsymbol{x}$の任意の1成分を上下限制約の範囲で$\pm1$した解の集合となります．

*3:ここでの近接性・集中性はともに本記事独自の定義です．

*4:MIPLIB 2017の難易度分類によれば，2021/9/21時点でeilC76-2は"easy"（商用ソルバで1時間以内に最適解が得られる），t1717は"open"（最適解が知られていない）となっています．

メタヒューリスティクスによる汎用整数計画ソルバーの開発

数理最適化

はじめに

メタヒューリスティクスベースの整数計画ソルバーをC++で開発しています．性能面・機能面ともに改善の余地はまだまだあるのですが，当初自分が思い描いたものがだいぶかたちになってきたということもあり，一度ご紹介したいと思います．

プログラムはオープンソースとして開発しており，ソースコード・ドキュメントは以下のGithubリポジトリで管理しています． github.com

開発したソルバーの概要と特徴

PRINTEMPS は，C++で設計・実装された線形／非線形整数計画問題を近似的に解く汎用モデラー／ソルバーです*1．アルゴリズムとしてはメタヒューリスティクス，具体的には文献[1]で提案されているペナルティ係数を動的に調整するタブーサーチ法を採用しており*2，分枝限定法に基づくMIPソルバーで解けない問題群に対し，厳密解にこだわらず「そこそこ良い解」を得たい局面での適用を想定しています*3．また前処理による変数・制約条件の除去や補助メモリを用いた高速な近傍解評価，解改善の見込みのない近傍操作の事前除去など，計算効率化の手法も取り入れています．

PRINTEMPSの特徴は以下のとおりです．

  • 可搬性：ヘッダオンリーライブラリとして実装されており，他の商用あるいはオープンソースライブラリにも依存していないため，必要なヘッダファイルを単純にコピーするだけで自作プログラムに組み込むことが可能
  • モデリングの直観性：ソルバーとあわせてモデリング環境も提供しており，プログラム上で数式を記述するかたちで問題のモデリングが可能*4
  • 近傍定義の拡張性：変数や問題構造に応じて適切な近傍定義*5を自動的に抽出するほか，ユーザ定義の近傍を採用することも可能

使い方

ダウンロード

上述のGithubリポジトリのmasterブランチをCloneしていただくか，Releaseから最新アーカイブをダウンロードします．

インストール

リポジトリ直下（あるいはアーカイブを解凍して展開されるディレクトリの直下）にあるprintempsディレクトリ以下を適当な場所にコピーしていただければOKです．

サンプル

サンプルとして，以下のような簡単な整数計画問題[2]を考えます： \begin{split} \mathrm{(P1)}: &\underset{x}{\mathrm{minimize}} \enspace &&&x_1 + 10 &x_2 \\ &\mathrm{subject\,to} \enspace &&66\, &x_1 + 14 &x_2 \ge 1430, \\ &&-&82\, &x_1 + 28 &x_2 \ge 1306, \end{split} $$ \qquad x_1, x_2 \in \mathbb{Z}. $$ 本問題をPRINTEMPSを用いてモデリング・求解するコードは以下のとおりとなります．

#include <printemps.h>
int main(void) {
    // (1) モデリング
    printemps::model::IPModel model;

    auto& x = model.create_variables("x", 2);
    auto& g = model.create_constraints("g", 2);

    g(0) =  66 * x(0) + 14 * x(1) >= 1430;
    g(1) = -82 * x(0) + 28 * x(1) >= 1306;
    model.minimize(x(0) + 10 * x(1));

    // (2) ソルバー実行（最適化）
    auto result = printemps::solver::solve(&model);

    // (3) 計算結果へのアクセス
    auto objective = result.solution.objective();
    auto variables = result.solution.variables("x");
    std::cout << "objective = " << objective << std::endl;
    std::cout << "x(0) = " << variables.values(0) << std::endl;
    std::cout << "x(1) = " << variables.values(1) << std::endl;

    return 0;
}

上のコードをコンパイルして実行すると以下の結果が標準出力として得られます．

objective = 707
x(0) = 7
x(1) = 70

リポジトリにはこのほかにもナップサック問題，ビンパッキング問題，数独，2次割当問題のサンプルを用意しています．example/ディレクトリ以下をご参照ください．モデリングを効率よくおこなうため，上のサンプル内で用いた記述法のみならず，複数の変数の和や，パラメータベクトルと変数ベクトルの内積などに対する簡単な記述法も備えています．

コンパイル

C++17に対応したC++コンパイラであればプラットフォームによらずコンパイル可能です（ただし以下の説明ではLinux, macOSを想定します）．たとえば，リポジトリに含まれるsample/knapsack.cppをg++を用いてコンパイル・ビルドする場合は以下のコマンドを実行します．

$g++ -std=c++17 -O3 -I path/to/printemps [-fopenmp] sample/knapsack.cpp -o knapsack.exe

ただしpath/to/printempsはPRINTEMPSのインストール先ディレクトリです．OpenMP有効化フラグ[-fopenmp]は必須でありませんが，マルチコア環境下ではこれを有効化することで近傍操作生成・近傍解評価などが並列化され，計算時間が短縮されます．

オプション・パラメータ設定

Solver Option Guideに示すとおり，PRINTEMPSには多数のオプション・パラメータがありますが，基本的には下表に示す計算時間や表示形式に係る項目の調整でじゅうぶんと思います．

オプション名 型 デフォルト 説明
iteration_max int 100 全体でのタブーサーチの外側反復回数
time_max double 120.0 全体での計算時間制限[sec]
output.verbose printemps::option::verbose None 標準出力へのログ出力レベル
None:なにも表示しない
Warning: 警告のみ表示
Outer:警告に加え， 各タブーサーチの外側反復の結果を表示
Full:タブーサーチの内側反復の結果も含めすべて表示

スタンドアロンソルバー

整数変数のみを含むMPS(Mathematical Programming System)ファイルに記述された問題を解くスタンドアロンソルバーも用意しており，以下のコマンドでコンパイル・ビルド可能です*6 ．

$g++ -std=c++17 -O3 -I path/to/printemps [-fopenmp] application/mps_solver/main.cpp -o mps_solver.exe

ただしpath/to/printempsはそれぞれPRINTEMPSのインストール先ディレクトリです． ビルドして得られたソルバーを用いてMPSファイルに記述された最適化問題の求解をおこなう場合，以下のコマンドを実行します．

$./mps_solver.exe mps_file [-p option_file]

mps_fileは解きたい問題が記述されたMPSファイルのパスです．-p option_fileは任意であり，オプション・パラメータをJSONファイル経由で指定できます．必要に応じて以下のJSONをテンプレートとしてお使いください．

{
    "iteration_max": 100,
    "time_max": 120.0,
    "output": {
        "verbose": "Off"
    }
}

ドキュメント

ドキュメントとして以下の2つを用意しています．

  • Starter Guide：全体にわたっての使用方法として，モデリング方法，最適化計算実行方法，計算結果へのアクセス方法について記述したもの
  • Solver Option Guide：オプションの一覧とその説明・デフォルト値について示したもの

非線形の目的関数・制約条件の定義方法や，ユーザ定義の近傍の定義方法については申し訳ありませんがStarter Guideには未記載です．これらを使用した計算をおこなう場合，2次割当問題のサンプルをご参考としていただければ幸いです．

ベンチマーク

MIPLIB 2017の整数計画問題インスタンスを用いた性能ベンチマークもおこなっています． 詳細なベンチマーク結果についてはこちらをご参照ください．

ライセンス

MITライセンスでの配布としています．

おわりに

PRINTEMPSはおもに実務における数理最適化業務を効率化することを目的として開発しています．数理最適化の業務は，

  • Step 1: 実問題を最適化問題としてモデリング（定式化）し，
  • Step 2: アルゴリズムを開発して（あるいはソルバーを用いて）問題を解き，
  • Step 3: 得られた解を検証し，問題がなければ解をなんらかのかたちで実行する．そうでなければStep 1へ戻る．

というプロセスを経ることが多いです．このプロセスが一回で完了することは稀であり，ほとんどの場合，解の検証で明らかになった制約条件の抜け漏れ反映などにより，Step 1〜Step 3のプロセスを複数回繰り返すこととなります．ここでStep 2の求解に際して，定式化された問題が分枝限定法ベースの汎用ソルバーで容易に解ける問題であるのならばよいのですが，実務では分枝限定法では手に負えない「厄介な」構造*7をもつ問題も多く見られます．このような問題たちに対して，とくに検討の端緒において，専用アルゴリズムを設計・実装するなどの手間をかけずに「そこそこの解」を求めたい，という局面は頻繁にあります．PRINTEMPSはこのような局面を想定して開発したソルバーであり，とくに「手軽さ」と「汎用性」を重視した作りとなっています．

現状では性能や速度については改善の余地も大きく，集合分割問題など等式制約条件を多く含む問題に弱いなどの弱点もありますが，引き続き頑張って改良を進めていきます！*8

参考文献

修正履歴

  • 2020/11/24 ソフトウェア名の変更に伴い記述を変更しました．またMIPLIB 2017のオープンインスタンス暫定値更新に関して注記を加筆しました．
  • 2020/12/1 章構成を修正しつつ，ベンチマーク結果について加筆しました．
  • 2020/12/5 本文の記述を微修正しました。また本ソルバを使う上での定式化のポイントについて注記を加筆しました．
  • 2021/4/22 v1.6.0バージョンアップにあわせて内容を改訂しました。
  • 2021/6/27 v1.6.3バージョンアップにあわせて内容を改訂しました。
  • 2022/8/31 v2.0.0バージョンアップにあわせて内容を改訂しました。

*1:ただし，高速化処理など多くの工夫は線形整数計画問題に特化するかたちで実装されており，特段の理由がなければ線形整数計画としてモデリング・求解することをおすすめします．

*2:商用ソルバーとしてはNTTデータ数理システムのNumerical Optimizerも同法に基づいたアルゴリズムを提供しています．当然ながら本ソルバーよりも高性能です．

*3:ただし，MIPソルバーが得意とする定式化と本ソルバーが得意とする定式化はかならずしも同じではありません．本ソルバーを用いる場合，等式制約条件をなるべく使わない定式化が望ましいです．

*4:モデリングの仕様についてはSIMPLEとPuLPの影響を受けています．

*5:0-1変数については1-flip近傍，その他整数変数については±1近傍および(最大値(最小値)+現在値)/2近傍が自動的に定義されており，これらがデフォルト近傍となります．このほかにもMIPLIB2017の制約条件区分に記載されたAggregation, Precedence, Variable Bound, Set Partitioningなど特殊な構造の制約条件が存在する場合，これらに特化した近傍が追加されます．ただし，問題によっては近傍数が莫大となるので，デフォルトでは一部の近傍はオフとしています．

*6:MakeおよびCMakeがインストールされた環境下では「$make -f makefile/Makefile.application」を実行すれば簡易にコンパイル・ビルドできます．

*7:たとえば「最大値最小化」とか「平準化」とか…．

*8:改良のなかでMIPLIB 2017のオープンインスタンスのひとつであるcdc 7-4-3-2, scpj4scip, scpl4, scpm1, scpn2の暫定値を更新しており，また他の複数のインスタンスに対しても既知の暫定解と同等の解を得ることに成功しています．

Benders分解法

数理最適化

はじめに

Benders分解法[1]とは，特定の構造をもつ大規模な数理最適化問題を解く手法のひとつです．Benders分解法では，解きたい最適化問題（原問題）を，それより小さな規模の上位問題と下位問題に分割し，これらの問題を交互に繰り返し解くことで原問題の最適解を求めます．Benders分解法は，原問題において一部の変数を固定すると，残りの変数に関する最適化問題が線形計画問題となるような問題に対して有効なアルゴリズムとして知られていますが，Benders分解法そのものを解説した日本語の情報源は数少なく，私の知るかぎり書籍[2]-[5]やウェブサイト[6][7]などに限られています．

本記事では，これらの書籍やウェブサイトを参考としつつも，個人的に重要と思うポイントを強調しつつ，Benders分解法の基本的な考え方やアルゴリズムについて自分なりに整理していきたいと思います．

本記事で議論する最適化問題の定式化

本記事では，以下のかたちで記述される最適化問題を題材とします：

\begin{align}
(\mathrm{P}): \underset{\boldsymbol{x}, \boldsymbol{y}}{\mathrm{minimize}} \, & \boldsymbol{c}^{\top}\boldsymbol{x} + f(\boldsymbol{y}) \tag{1} \\
\mathrm{subject\,to} \, &\boldsymbol{A}\boldsymbol{x} + \boldsymbol{g}(\boldsymbol{y}) \ge \boldsymbol{b}, \tag{2} \\
& \boldsymbol{x} \ge \boldsymbol{0}, \tag{3} \\
& \boldsymbol{y} \in \mathcal{Y}. \tag{4}
\end{align}

ただし，$\boldsymbol{x}, \boldsymbol{y}$は決定変数で，それぞれ$N$次元の非負連続変数ベクトル，集合$\mathcal{Y}$内の要素とします．$\boldsymbol{c}, \boldsymbol{b}, \boldsymbol{A}$は適当なサイズのベクトル，行列とします．また$f,\boldsymbol{g}$はそれぞれ$\mathcal{Y}$を定義域とする適当なスカラ，ベクトル関数とします．

Benders分解法の考えかた

最適化問題$(\mathrm{P})$に対して，その問題構造を利用した分解解法を考えます．$(\mathrm{P})$において，決定変数$\boldsymbol{y}$を適当に固定すると，残りの決定変数$\boldsymbol{x}$に関する最適化問題は線形計画問題となり，容易に解けるという点に着目します．そこで，$(\mathrm{P})$を解くアルゴリズムのプロトタイプとして，以下のような計算手順を考えます（最終的にはやや異なる計算手順となります）．

  • Step 1: 適当な上位問題を解き，$\bar{\boldsymbol{y}} \in \mathcal{Y}$を決定する．
  • Step 2: Step 1で決定した$\bar{\boldsymbol{y}}$のもとで，下位問題

\begin{align}
(\mathrm{P}(\bar{\boldsymbol{y}})): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \boldsymbol{c}^{\top}\boldsymbol{x} \tag{5} \\
\mathrm{subject\,to} \, &\boldsymbol{A}\boldsymbol{x} + \boldsymbol{g}(\bar{\boldsymbol{y}}) \ge \boldsymbol{b}, \tag{6} \\
& \boldsymbol{x} \ge \boldsymbol{0}. \tag{7}
\end{align}

を解き，その解を$\boldsymbol{x}^{\ast}(\bar{\boldsymbol{y}})$とする．

  • Step 3: $(\boldsymbol{x}^{\ast}(\bar{\boldsymbol{y}}), \bar{\boldsymbol{y}})$について，最適性の証拠が得られていればこれを最適解として計算を終了する．そうでなければ下位問題の最適化結果をフィードバックしつつStep 1へ戻る．

上述の計算手順の構築にあたっては，以下の2点が技術的課題となります．

  • (a) 上位問題をどのように定式化するか？
  • (b) 下位問題の最適化結果を上位問題にどのようにフィードバックするか？

ここで，下位問題$(\mathrm{P}(\bar{\boldsymbol{y}}))$の双対問題

\begin{align}
(\mathrm{D}(\bar{\boldsymbol{y}})): \underset{\boldsymbol{\lambda}}{\mathrm{maximize}} \,& (\boldsymbol{b} - \boldsymbol{g}(\bar{\boldsymbol{y}}) )^{\top}\boldsymbol{\lambda} \tag{8} \\
\mathrm{subject\,to} \,& \boldsymbol{A}^{\top} \boldsymbol{\lambda} \le \boldsymbol{c}, \tag{9} \\
& \boldsymbol{\lambda} \ge \boldsymbol{0}. \tag{10}
\end{align}

を考え，$(\mathrm{P}(\bar{\boldsymbol{y}}))$と$(\mathrm{D}( \bar{\boldsymbol{y}}))$の実行可能解集合をそれぞれ

\begin{align}
\mathcal{X}(\bar{\boldsymbol{y}}) &= \left\{ \boldsymbol{x} \mid \boldsymbol{A}\boldsymbol{x} + \boldsymbol{g}(\bar{\boldsymbol{y}}) \ge \boldsymbol{b}, \boldsymbol{x} \ge \boldsymbol{0} \right\} \tag{11} \\
\mathcal{L} &= \{ \boldsymbol{\lambda} \mid \boldsymbol{A}^{\top} \boldsymbol{\lambda} \le \boldsymbol{c}, \boldsymbol{\lambda} \ge \boldsymbol{0} \} \tag{12}
\end{align}

と書くこととします．ここで，$(\mathrm{P}(\bar{\boldsymbol{y}}))$の実行可能解集合は上位問題の解$\bar{\boldsymbol{y}}$に依存するいっぽうで，$(\mathrm{D}( \bar{\boldsymbol{y}}))$の実行可能解集合は$\bar{\boldsymbol{y}}$に依存しないという点に注意します．

以降では$(\mathrm{P}(\bar{\boldsymbol{y}}))$を「下位主問題」，$(\mathrm{D}(\bar{\boldsymbol{y}}))$を「下位双対問題」とよぶこととし，$\mathcal{L} \neq \emptyset$とします．また，議論を簡単にするため，任意の上位問題の解$\bar{\boldsymbol{y}}\in \mathcal{Y}$に対して$(\mathrm{P}(\bar{\boldsymbol{y}}))$は実行可能解をもつと仮定します．本仮定のもとで，線形計画問題の弱双対定理より，任意の$\bar{\boldsymbol{y}}\in \mathcal{Y}, \boldsymbol{x} \in \mathcal{X}(\bar{\boldsymbol{y}})$と$\boldsymbol{\lambda} \in \mathcal{L}$に対し，
$$
(\boldsymbol{b} - \boldsymbol{g}(\bar{\boldsymbol{y}}))^{\top} \boldsymbol{\lambda} \le \boldsymbol{c}^{\top}\boldsymbol{x} \tag{13}
$$

がなりたちます．また，$(\mathrm{P}(\bar{\boldsymbol{y}}))$と$(\mathrm{D}( \bar{\boldsymbol{y}}))$の最適解をそれぞれ$\boldsymbol{x}^{\ast}(\bar{\boldsymbol{y}}),\boldsymbol{\lambda}^{\ast}(\bar{\boldsymbol{y}})$，最適値をそれぞれ$f^{\ast}(\mathrm{P}(\bar{\boldsymbol{y}})), f^{\ast}(\mathrm{D}(\bar{\boldsymbol{y}}))$としたとき，線形計画問題の強双対定理より
$$
f^{\ast}(\mathrm{D}(\bar{\boldsymbol{y}})) = (\boldsymbol{b} - \boldsymbol{g}(\bar{\boldsymbol{y}}))^{\top} \boldsymbol{\lambda}^{\ast}(\bar{\boldsymbol{y}}) = \boldsymbol{c}^{\top}\boldsymbol{x}^{\ast}(\bar{\boldsymbol{y}}) = f^{\ast}(\mathrm{P}(\bar{\boldsymbol{y}})) \tag{14}
$$

がなりたちます．ここで，(13)式と(14)式が示す性質

  • $(\mathrm{D}(\bar{\boldsymbol{y}}))$の任意の実行可能解の目的関数値は$(\mathrm{P}(\bar{\boldsymbol{y}}))$の任意の実行可能解の目的関数値以下である
  • $(\mathrm{D}(\bar{\boldsymbol{y}}))$と$(\mathrm{P}(\bar{\boldsymbol{y}}))$の最適値は一致する

を用いると，原問題$(\mathrm{P})$の最適な$\boldsymbol{y}$を求める上位問題は，$(\mathrm{D}(\bar{\boldsymbol{y}}))$を内包するかたちで
\begin{align}
(\mathrm{MP}): \underset{\boldsymbol{y}}{\mathrm{minimize}} \, & \max_{\boldsymbol{\lambda} \in \mathcal{L}}(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}))^{\top} \boldsymbol{\lambda} + f(\boldsymbol{y}) \tag{15} \\
\mathrm{subject\,to} \, &\boldsymbol{y} \in \mathcal{Y}. \tag{16}
\end{align}

と定式化することができます．

上位問題$(\mathrm{MP})$の最適解$\boldsymbol{y}^{\ast}$が得られれば，$\boldsymbol{y}^{\ast}$のもとで下位主問題$(\mathrm{P}(\boldsymbol{y}^{\ast}))$を解くことで（$\boldsymbol{y}^{\ast}$とあわせて）$(\mathrm{P})$の最適解を得ることができます．そこで当面は$(\mathrm{MP})$を解く方法を考えることとします．

上位問題$(\mathrm{MP})$は，補助変数$\zeta \in \mathbb{R}$を用いて，
$$
\begin{align}
(\mathrm{MP}'): \underset{\zeta, \boldsymbol{y}}{\mathrm{minimize}} \, & \zeta + f(\boldsymbol{y}) \tag{17} \\
\mathrm{subject\,to} \, &(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}))^{\top} \boldsymbol{\lambda}\le \zeta \quad(\forall \boldsymbol{\lambda} \in \mathcal{L}), \tag{18} \\
& \zeta > -\infty，\tag{19} \\
&\boldsymbol{y} \in \mathcal{Y}. \tag{20}
\end{align}
$$

と書き換えることができます．ただし$\mathcal{L}$の要素数は無限にあり，$(\mathrm{MP}')$を直接解くことは困難です．そこで，必要に応じて逐次$\boldsymbol{\lambda} \in \mathcal{L}$を求めて制約条件を追加していく計算手順を考えることとします．

上位問題$(\mathrm{MP}')$のうち，一部の$\mathcal{C} \subseteq \mathcal{L}$のみについて制約条件として考慮した緩和問題
$$
\begin{align}
(\mathrm{MP}'(\mathcal{C})): \underset{\zeta, \boldsymbol{y}}{\mathrm{minimize}} \, & \zeta + f(\boldsymbol{y}) \tag{21} \\
\mathrm{subject\,to} \, &(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}))^{\top} \boldsymbol{\lambda}\le \zeta \quad(\forall \boldsymbol{\lambda} \in \mathcal{C}), \tag{22} \\
& \zeta > -\infty, \tag{23} \\
&\boldsymbol{y} \in \mathcal{Y}. \tag{24}
\end{align}
$$

を考え，その最適解を$(\zeta^{\ast}(\mathcal{C}), \boldsymbol{y}^{\ast}(\mathcal{C}))$とします．また，$\boldsymbol{y}^{\ast}(\mathcal{C})$のもとでの下位双対問題$(\mathrm{D}(\boldsymbol{y}^{\ast}(\mathcal{C})))$の最適解を$\boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C}))$とします．$(\mathrm{D}(\boldsymbol{y}^{\ast}(\mathcal{C})))$は，$\boldsymbol{\lambda} \in \mathcal{L}$のなかで$(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})))^{\top} \boldsymbol{\lambda}$を最大化する問題ですので，
$$
(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})))^{\top} \boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})) \le \zeta^{\ast}(\mathcal{C}) \tag{25}
$$

がなりたつならば，緩和問題$(\mathrm{MP}'(\mathcal{C}))$の解$(\zeta^{\ast}(\mathcal{C}), \boldsymbol{y}^{\ast}(\mathcal{C}))$は，(18)式を満足することから$(\mathrm{MP})$の最適解となります．なおこの場合，上述のとおり$\boldsymbol{y}^{\ast}(\mathcal{C})$のもとで下位主問題$(\mathrm{P}(\boldsymbol{y}^{\ast}(\mathcal{C})))$を解くことで$(\mathrm{P})$の最適解を得ることができます．いっぽう，
$$
(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})))^{\top} \boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})) > \zeta^{\ast}(\mathcal{C}) \tag{26}
$$

であるならば，$(\zeta^{\ast}(\mathcal{C}), \boldsymbol{y}^{\ast}(\mathcal{C}))$は(18)式を満足しないため，$\boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C}))$を$\mathcal{C}$の要素として加え（つまり新しい制約条件を追加し），$(\mathrm{MP}'(\mathcal{C}))$を解きなおす必要があります．

Benders分解法とは，以上の考え方をもとに，集合$\mathcal{C}$を更新しつつ，上位問題の緩和問題$(\mathrm{MP}'(\mathcal{C}))$と下位双対問題$(\mathrm{D}(\boldsymbol{y}^{\ast}(\mathcal{C})))$を交互に解くことで上位問題$(\mathrm{MP})$の最適解$\boldsymbol{y}^{\ast}$を求め，最後に$\boldsymbol{y}^{\ast}$のもとで下位主問題$(\mathrm{P}(\boldsymbol{y}^{\ast}))$を解くことで（$\boldsymbol{y}^{\ast}$とあわせて）原問題$(\mathrm{P})$の最適解$(\boldsymbol{x}^{\ast}, \boldsymbol{y}^{\ast})$を求めるアルゴリズムとなります．

Benders分解法のアルゴリズム

前節の議論を踏まえ，Benders分解法のアルゴリズムを以下のとおりまとめます．

  • Step 1（初期化）: $\mathcal{C} = \emptyset$とする．
  • Step 2（上位緩和問題最適化）:上位問題の緩和問題

$$
\begin{align}
(\mathrm{MP}'(\mathcal{C})): \underset{\zeta, \boldsymbol{y}}{\mathrm{minimize}} \, & \zeta + f(\boldsymbol{y}) \tag{27} \\
\mathrm{subject\,to} \, &(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}))^{\top} \boldsymbol{\lambda}\le \zeta \quad(\forall \boldsymbol{\lambda} \in \mathcal{C}), \tag{28}\\
& \zeta > -\infty, \tag{29}\\
&\boldsymbol{y} \in \mathcal{Y}. \tag{30}
\end{align}
$$

を解き，その最適解を$(\zeta^{\ast}(\mathcal{C}), \boldsymbol{y}^{\ast}(\mathcal{C}))$とする．

  • Step 3（下位双対問題最適化）: Step 2で求めた$\boldsymbol{y}^{\ast}(\mathcal{C})$のもとで，下位双対問題

$$
\begin{align}
(\mathrm{D}(\boldsymbol{y}^{\ast}(\mathcal{C}))): \underset{\boldsymbol{\lambda}}{\mathrm{maximize}} \,& (\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})) )^{\top}\boldsymbol{\lambda} \tag{31}\\
\mathrm{subject\,to} \,& \boldsymbol{A}^{\top} \boldsymbol{\lambda} \le \boldsymbol{c}, \tag{32} \\
& \boldsymbol{\lambda} \ge \boldsymbol{0}. \tag{33}
\end{align}
$$

を解き，その最適解を$\boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C}))$とする．

  • Step 4（制約条件追加）: Step 2で求めた$\zeta^{\ast}(\mathcal{C})$とStep 3で求めた$\boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C}))$が

$$
(\boldsymbol{b} - \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})))^{\top} \boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})) \le \zeta^{\ast}(\mathcal{C}) \tag{34}
$$

を満たすならばStep 5へ進む．そうでないならば，
$$
\mathcal{C} := \mathcal{C} \cup \{ \boldsymbol{\lambda}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})) \} \tag{35}
$$

としてStep 2へ進む．

  • Step 5（下位主問題最適化）: Step 2で求めた$\boldsymbol{y}^{\ast}(\mathcal{C})$のもとで，下位主問題

$$
\begin{align}
(\mathrm{P}(\boldsymbol{y}^{\ast}(\mathcal{C}))): \underset{\boldsymbol{x}}{\mathrm{minimize}} \, & \boldsymbol{c}^{\top}\boldsymbol{x} \tag{36} \\
\mathrm{subject\,to} \, &\boldsymbol{A}\boldsymbol{x} + \boldsymbol{g}(\boldsymbol{y}^{\ast}(\mathcal{C})) \ge \boldsymbol{b}, \tag{37} \\
& \boldsymbol{x} \ge \boldsymbol{0}. \tag{38}
\end{align}
$$

を解き，その最適解を$\boldsymbol{x}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C}))$とする．$(\boldsymbol{x}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})), \boldsymbol{y}^{\ast}(\mathcal{C}))$を最適化問題$(\mathrm{P})$の最適解として出力し，アルゴリズムを終了する．

補足

近似解法としてのBenders分解法

前節のアルゴリズムを実行することで，適当な仮定のもとで，有限回の反復で原問題$(\mathrm{P})$の最適解が求まることが示されています（文献[1]-[3]など）．ただし，計算時間の制約などから，途中で計算を打ち切る必要が生じる場合も考えられます．このような場合，アルゴリズムのStep 3において，下位双対問題$(\mathrm{D}(\boldsymbol{y}^{\ast}(\mathcal{C})))$とあわせて下位主問題$(\mathrm{P}(\boldsymbol{y}^{\ast}(\mathcal{C})))$も解いておくことで，毎回の反復において$(\mathrm{P})$の実行可能解を得ることができます．ここで得られる実行可能解$(\boldsymbol{x}^{\ast}(\boldsymbol{y}^{\ast}(\mathcal{C})), \boldsymbol{y}^{\ast}(\mathcal{C}))$に対して，
$$
\begin{align}
\boldsymbol{c}^{\top}\boldsymbol{x}(\boldsymbol{y}^{\ast}(\mathcal{C})) + f(\boldsymbol{y}^{\ast}(\mathcal{C})) \tag{39}
\end{align}
$$

は原問題$(\mathrm{P})$の上界値をあたえます．また，Step 1で計算される上位問題の緩和問題$(\mathrm{MP}'(\mathcal{C}))$の最適値は$(\mathrm{P})$の下界値をあたえます．これらは計算の反復に対してそれぞれ非増加，非減少となります．よって，各反復におけるギャップ（上界値と下界値の差）は，
$$
\begin{align}
\boldsymbol{c}^{\top}\boldsymbol{x}(\boldsymbol{y}^{\ast}(\mathcal{C})) - \zeta^{\ast}(\mathcal{C}) \tag{40}
\end{align}
$$

で計算でき，最適解に対してどの程度の近似解が得られているかを逐次チェックすることができます．

下位問題が実行不可能となりうる問題に対するBenders分解法

本記事では「上位問題の解によらず下位主問題・双対問題が実行可能解をもつ」という比較的強い仮定のもとで議論を進めましたが，上位問題の解によっては下位主問題が実行不可能となる場合も考えられます．そのような場合に対するBenders分解法については文献[1]-[3]などに詳述されています．

下位問題がさらに複数の問題に分割できる場合

Benders分解法がとくに威力を発揮する問題の例として「上位問題においていくつかの決定変数を固定することによって，下位問題が複数の小さな問題に分割できる」構造の問題があげられます．具体例として，以下の最適化問題を考えます．
$$
\begin{align}
(\mathrm{Pm}): \underset{\{\boldsymbol{x}_{i}\}_{i\in \mathcal{I}}, \boldsymbol{y}}{\mathrm{minimize}} \, & \sum_{i \in \mathcal{I}}\boldsymbol{c}_{i}^{\top}\boldsymbol{x}_{i} + f(\boldsymbol{y}) \tag{41} \\
\mathrm{subject\,to} \, &\boldsymbol{A}_{i}\boldsymbol{x}_{i} + \boldsymbol{g}_{i}(\boldsymbol{y}) \ge \boldsymbol{b}_{i} \quad (i \in \mathcal{I}), \tag{42} \\
& \boldsymbol{x}_{i} \ge \boldsymbol{0}\quad (i \in \mathcal{I}), \tag{43} \\
& \boldsymbol{y} \in \mathcal{Y}. \tag{44}
\end{align}
$$

ただし$\mathcal{I}$は有限個の要素をもつ添字集合とします．本問題をBenders分解法で解く際，上位問題において$\boldsymbol{y} = \bar{\boldsymbol{y}}$と固定すると，下位主問題は
$$
\begin{align}
(\mathrm{Pm}(\bar{\boldsymbol{y}})): \underset{\{\boldsymbol{x}_{i}\}_{i\in \mathcal{I}}}{\mathrm{minimize}} \, & \sum_{i \in \mathcal{I}}\boldsymbol{c}_{i}^{\top}\boldsymbol{x}_{i} \tag{45} \\
\mathrm{subject\,to} \, &\boldsymbol{A}_{i}\boldsymbol{x}_{i} + \boldsymbol{g}_{i}(\boldsymbol{\bar{y}}) \ge \boldsymbol{b}_{i} \quad (i \in \mathcal{I}), \tag{46} \\
& \boldsymbol{x}_{i} \ge \boldsymbol{0}\quad (i \in \mathcal{I}). \tag{47}
\end{align}
$$

となり，目的関数，制約条件ともに添字$i$ごとに独立していることがわかります．すなわち，$(\mathrm{Pm}(\bar{\boldsymbol{y}}))$の最適解は，添字$i$に関する最適化問題
$$
\begin{align}
(\mathrm{Pm}_{i}(\bar{\boldsymbol{y}})): \underset{\boldsymbol{x}_{i}}{\mathrm{minimize}} \, & \boldsymbol{c}_{i}^{\top}\boldsymbol{x}_{i} \tag{48} \\
\mathrm{subject\,to} \, &\boldsymbol{A}_{i} \boldsymbol{x}_{i} + \boldsymbol{g}(\bar{\boldsymbol{y}}) \ge \boldsymbol{b}_{i}, \tag{49} \\
& \boldsymbol{x}_{i} \ge \boldsymbol{0}. \tag{50}
\end{align}
$$

を$i \in \mathcal{I}$に対して個別に解き，各問題の最適解を集約することで得られます．$(\mathrm{Pm}_{i}(\bar{\boldsymbol{y}})) (i \in \mathcal{I})$は$(\mathrm{Pm}(\bar{\boldsymbol{y}}))$よりも小さい最適化問題であり解きやすく，さらに互いに独立していることから，これらを並列計算で解くことも可能です．同様に，下位双対問題
$$
\begin{align}
(\mathrm{Dm}_{i}(\bar{\boldsymbol{y}})): \underset{\boldsymbol{\lambda}_{i}}{\mathrm{maximize}} \,& (\boldsymbol{b}_{i} - \boldsymbol{g}_{i}(\bar{\boldsymbol{y}}) )^{\top}\boldsymbol{\lambda}_{i} \tag{51} \\
\mathrm{subject\,to} \,& \boldsymbol{A}_{i}^{\top} \boldsymbol{\lambda}_{i} \le \boldsymbol{c}_{i}, \tag{52} \\
& \boldsymbol{\lambda_{i}} \ge \boldsymbol{0}. \tag{53}
\end{align}
$$

についても添字$i$ごとに個別に解くことができ，前節のアルゴリズムのStep 4（制約条件追加）は，$(\mathrm{Dm}_{i}(\bar{\boldsymbol{y}}))$の最適解を集約するかたちで実現できます．

おわりに

本記事ではBenders分解法の基本的な考え方とアルゴリズムについて，自分なりに整理してみました．個人的には，「下位問題の双対問題の実行解集合が上位問題の解に依存しない」 という問題構造の性質を活用する点がBenders分解法の一番重要なポイントであると考えています．

Benders分解法は線形計画問題に対する双対問題・双対定理を最大限に利用したアルゴリズムになっており，これらの理解がほぼ前提となっています．いっぽうでBenders分解法は，アルゴリズム設計に双対問題・双対定理を直接応用する好例であり，これらについて理解を深めるよい題材であるとも考えています．

本記事が少しでもご参考となれば幸いでございます．

参考文献